| Occupation | 1990 | 2010 |
|---|---|---|
| Secretary | ✓ | ✓ |
| Nurse | ✗ | ✓ |

Structurally Conditioned Diffusion Reproduces Skills-Based Stratification
How Skill Requirements Propagate — And Why They Preserve Hierarchies
Roberto Cantillan & Mauricio Bucca
Department of Sociology | Pontificia Universidad Católica de Chile
The Puzzle
What we know:
- Labor markets are organized around unequal occupations differing in skills, wages, and credentials
- A polarized skill space: socio-cognitive vs. sensory/physical domains align with education and wages
- A nested hierarchy: enabling capabilities sit higher, command wage premia, require longer education
What we don’t know:
How do skill requirements propagate between occupations — and why does this process reproduce hierarchies?

The Architecture We Build Upon
Polarization (Alabdulkareem et al. 2018)
- Skills cluster into two domains
- Socio-cognitive: high education, high wages
- Sensory/physical: lower education, lower wages
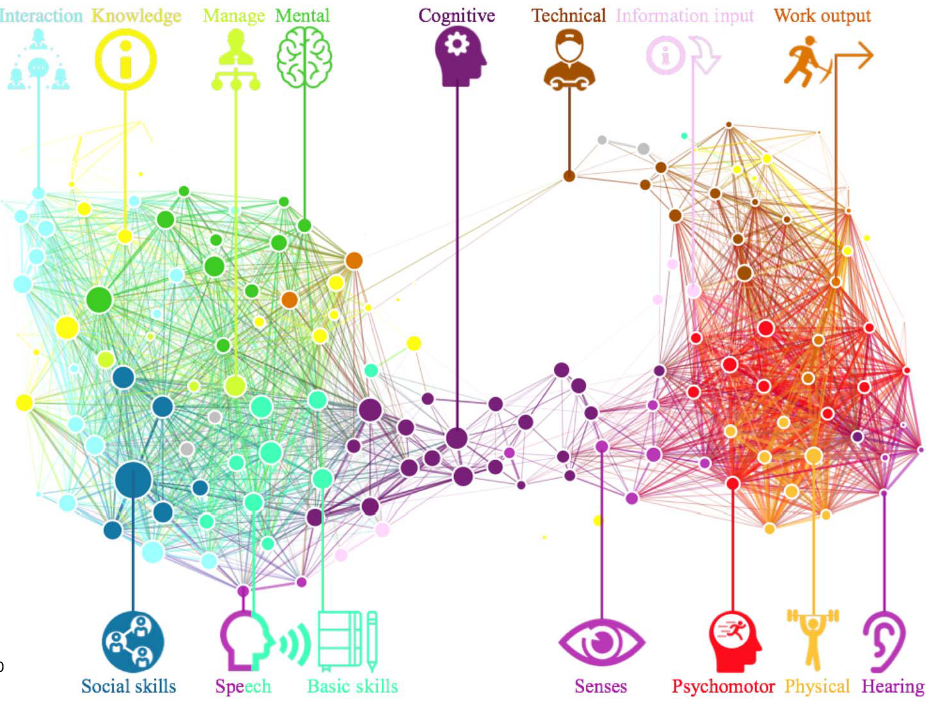
The Architecture We Build Upon
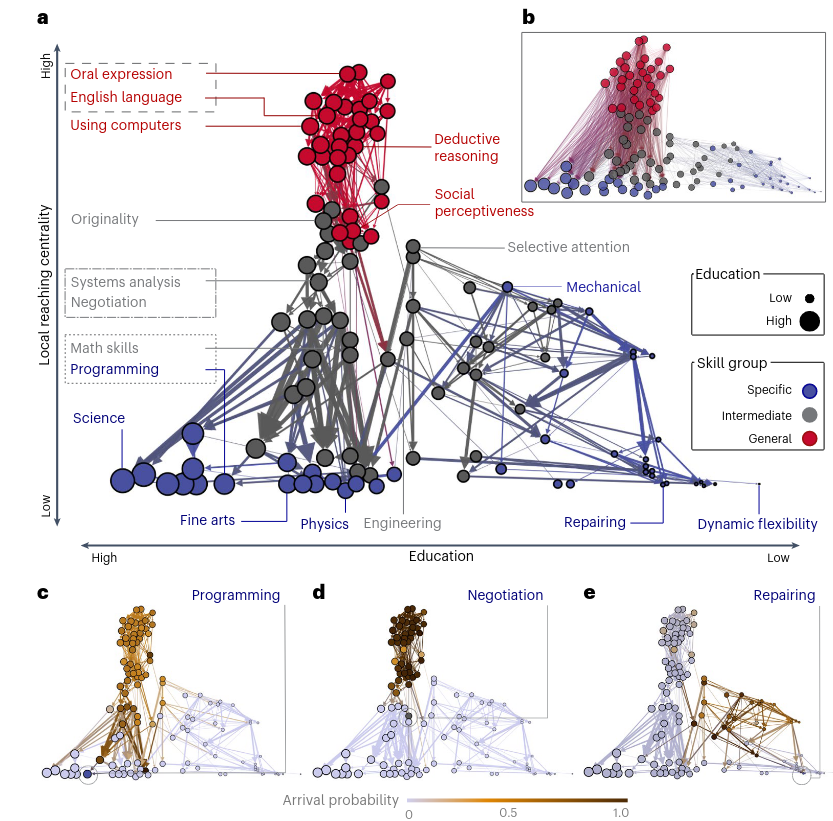
Nestedness (Hosseinioun et al. 2025)
- Asymmetric dependencies: some skills “enable” others
- Nested architecture has intensified over time
- Position in hierarchy predicts wages, automation risk
I. A GRAVITY MODEL FOR SKILL DIFFUSION
Skill diffusion as a gravity process
Skill specific diffusivity (g)
Masses (m)
Distance (d)
- Task similarity (symmetric)
- Status gap (asymmetric)
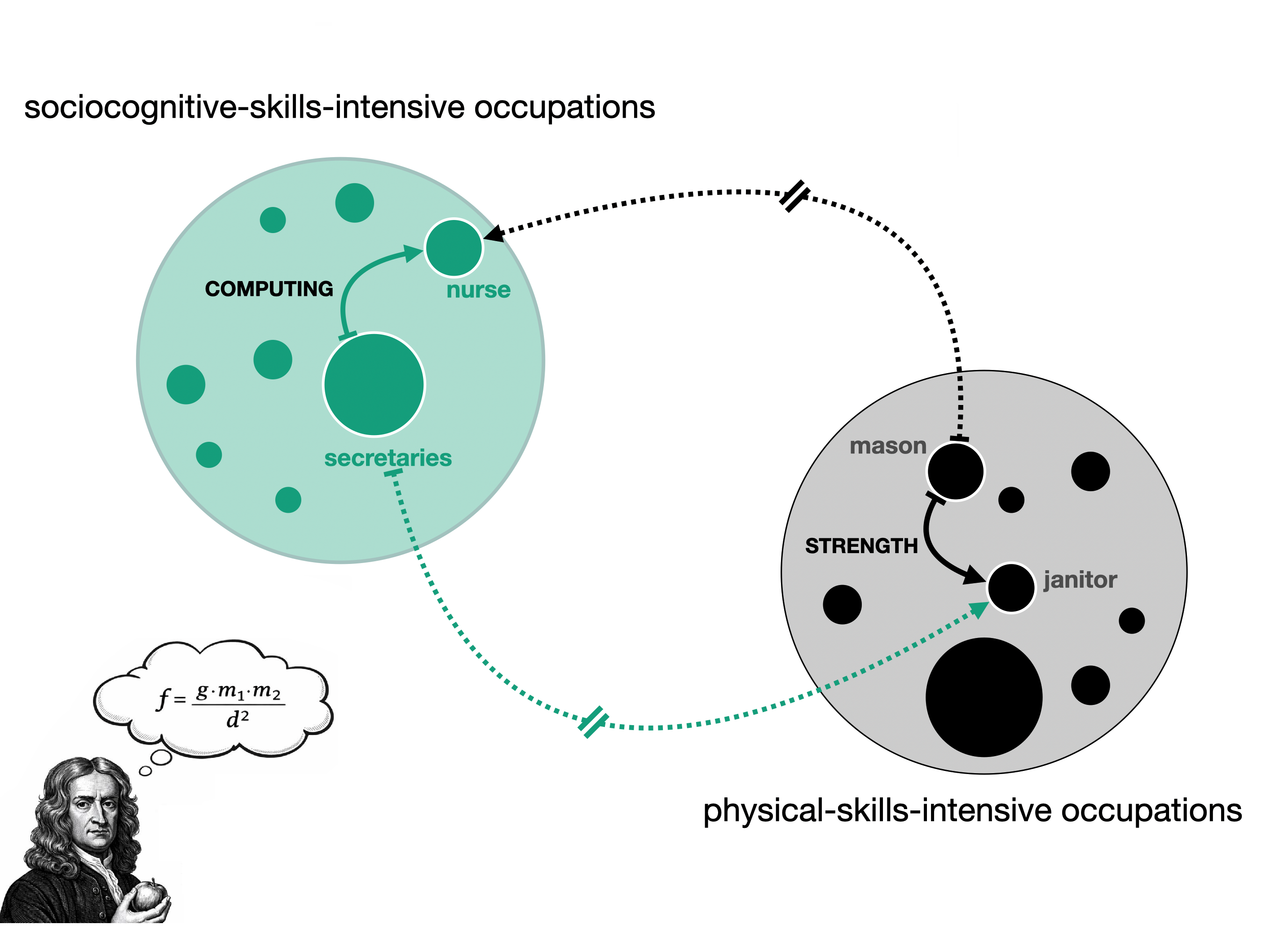
Our theory: Asimmetric trayectory channeling
Socio-cognitive requirements are preferentially adopted by occupations of higher status than the source, successfully climbing the status gradient.
Physical requirements face a structural “upward veto,” being predominantly relegated to adoption paths toward lower-status occupations.
This asymmetric dynamic would explain the observed polarized skill architecture of the labor market.
Our theory: Asimmetric trayectory channeling
Alternative accounts
- Skills travel between similar occupations: We control for occupational task relatedness (structural distance).
- Diffusion is driven by occupation size, not skills: We account for occupational “mass” using occupation fixed effects (Source and Target).
- Some skills travel more easily than others: We account for intrinsic diffusivity using skill-level fixed effects (\(g_s\)).
II. DATA & METHODS
Data
- O*NET 2015-2024 (161 skill taxonomy)
- BLS wages and education
- About 17M dyadic opportunities
Measures I
- Dependent Variable: Skill Adoption (\(Y_{ijs}\)). Where \(Y=1\) if a target (2024) adopts a skill previously held by a source (2015), and \(Y=0\) if the opportunity for adoption was not taken.
- Main Independent Variables:
- Wage Gap (Piecewise):
- \(\text{wage_gap}_{ij}{\uparrow} = \max(0, G_{ij})\)
- \(\text{wage_gap}_{ij}{\downarrow} = \min(0, G_{ij})\)
- Where \(G_{ij} = \log(\overline{W}_{target}) - \log(\overline{W}_{source})\)
- Wage Gap (Piecewise):
- Critical control variables:
- Structural Proximity: Occupational Task Relatedness calculated via cosine similarity
- Source, Target and Skill fixed effects.
Measures II
Skill type: Skill types might respond to wage gaps differently

The ATC Model
For each skill type, I estimate a linearized version of the gravity model
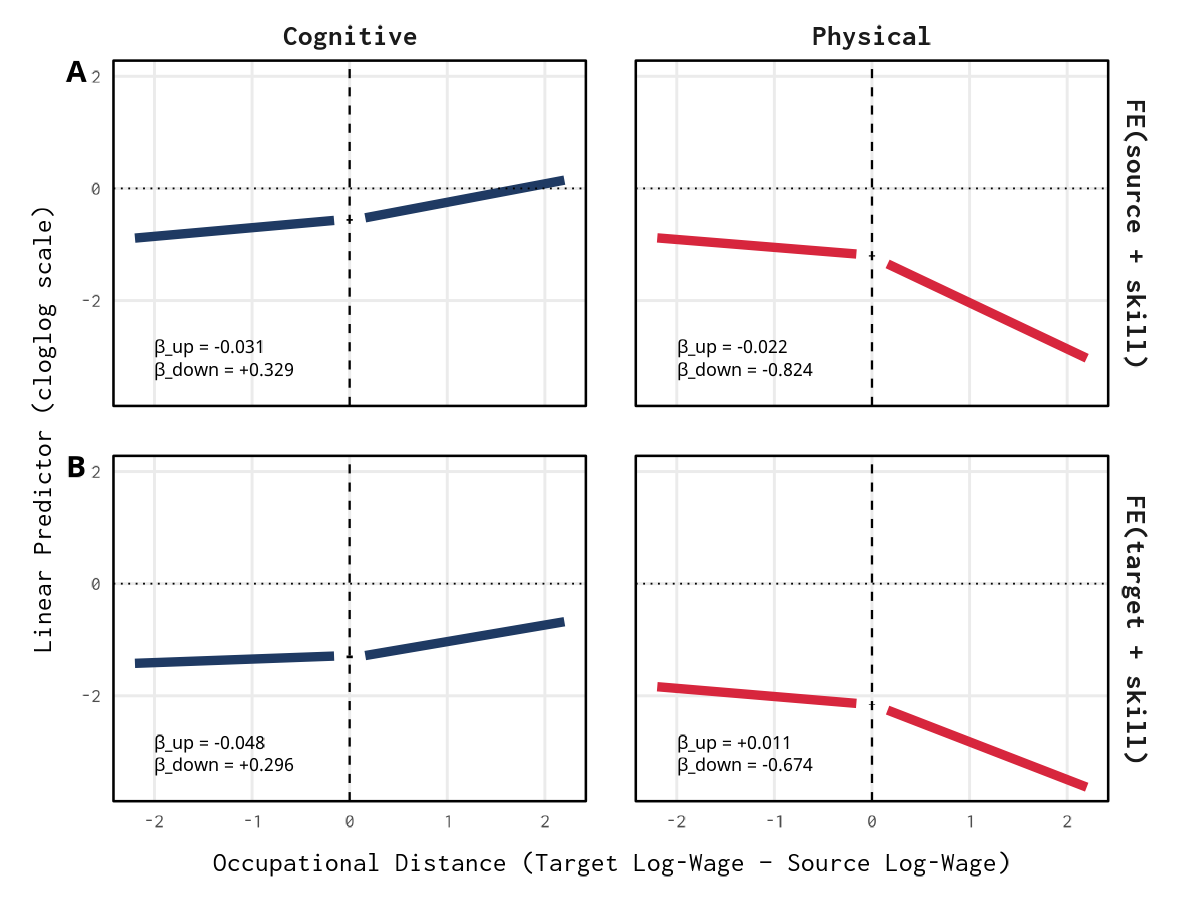
\[ \begin{aligned} \mathrm{logit}\,P(Y_{ijs}=1) = \, & \beta_{\text{up}}(\text{wage_gap}_{ij})^\uparrow + \beta_{\text{down}}(\text{wage_gap}_{ij})^\downarrow \\ & + \delta \cdot \text{relatedness}_{ij} \\ & + \text{source}_{i} / \text{target}_{j} + \text{skill}_{s} \end{aligned} \]
- \(\beta_{\text{up}}/ \beta_{\text{down}}\) measure the specific resistance (or facilitation) encountered when the target occupation has a higher (\(\uparrow\)) or lower (\(\downarrow\)) wage status than the source.
- \(\delta\) is the effect for the task-relatedness between occupations.
- \(\text{source}_i, \text{target}_j, \text{skill}_s\) are fixed effects measuring occupational emission/absorption mass and intrinsic “diffusivity” of each skill1.
III. FINDINGS
Raw Patterns
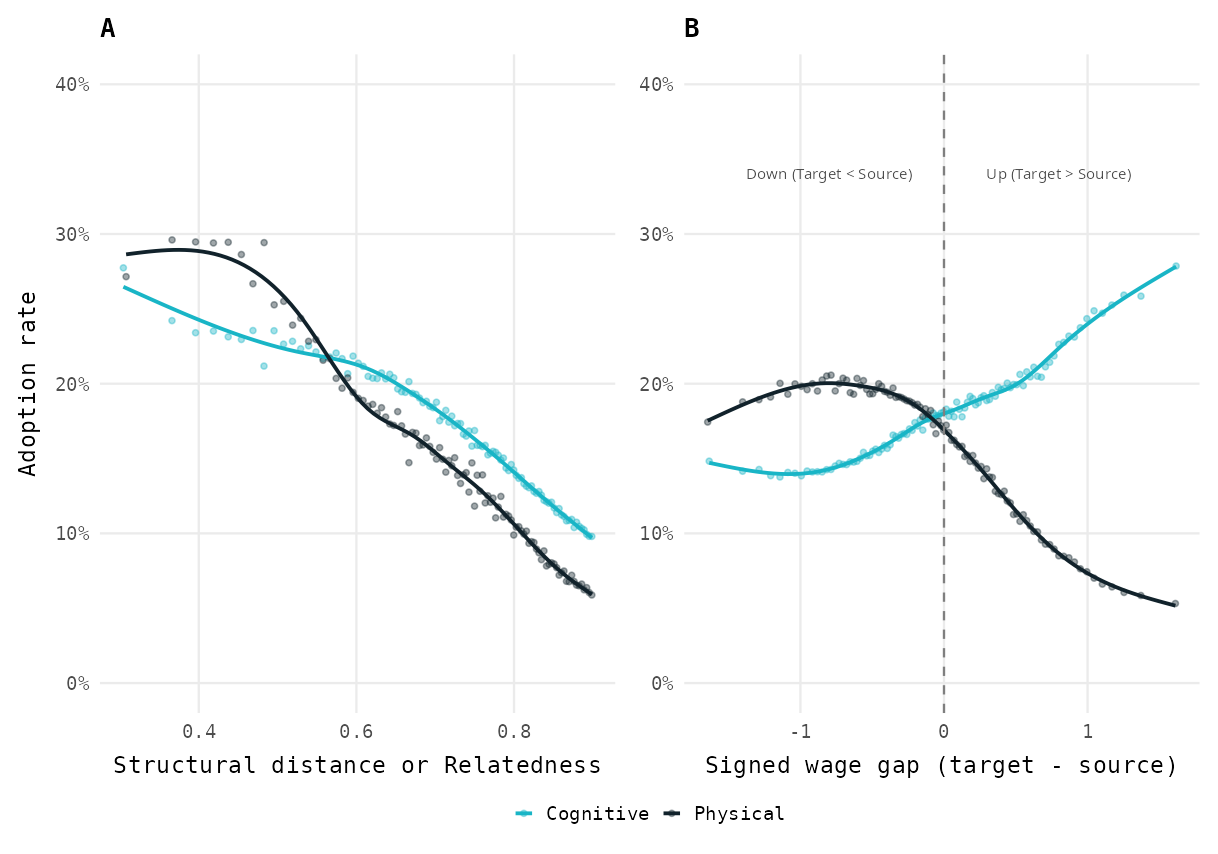
Polarized Diffusion: Flow Networks


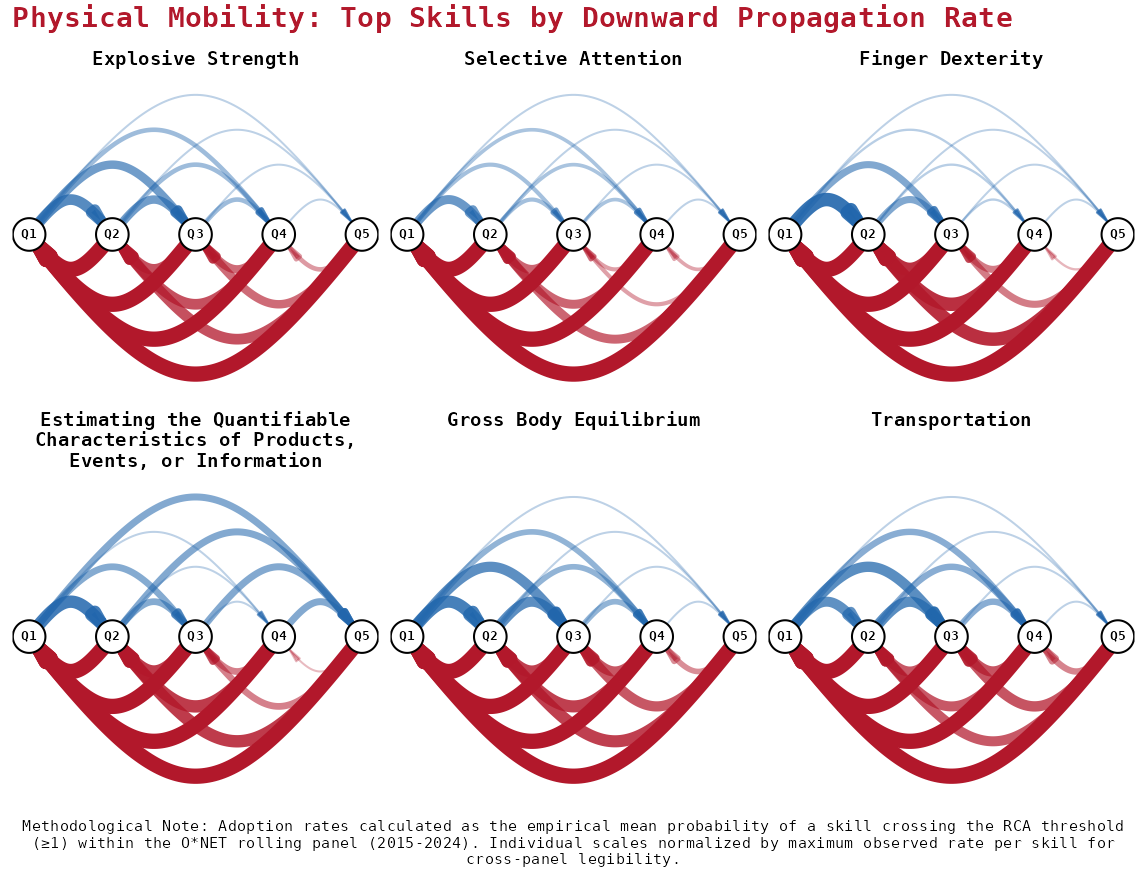
III. REGRESSION RESULTS
Asymmetric trajectory channeling by skill domain
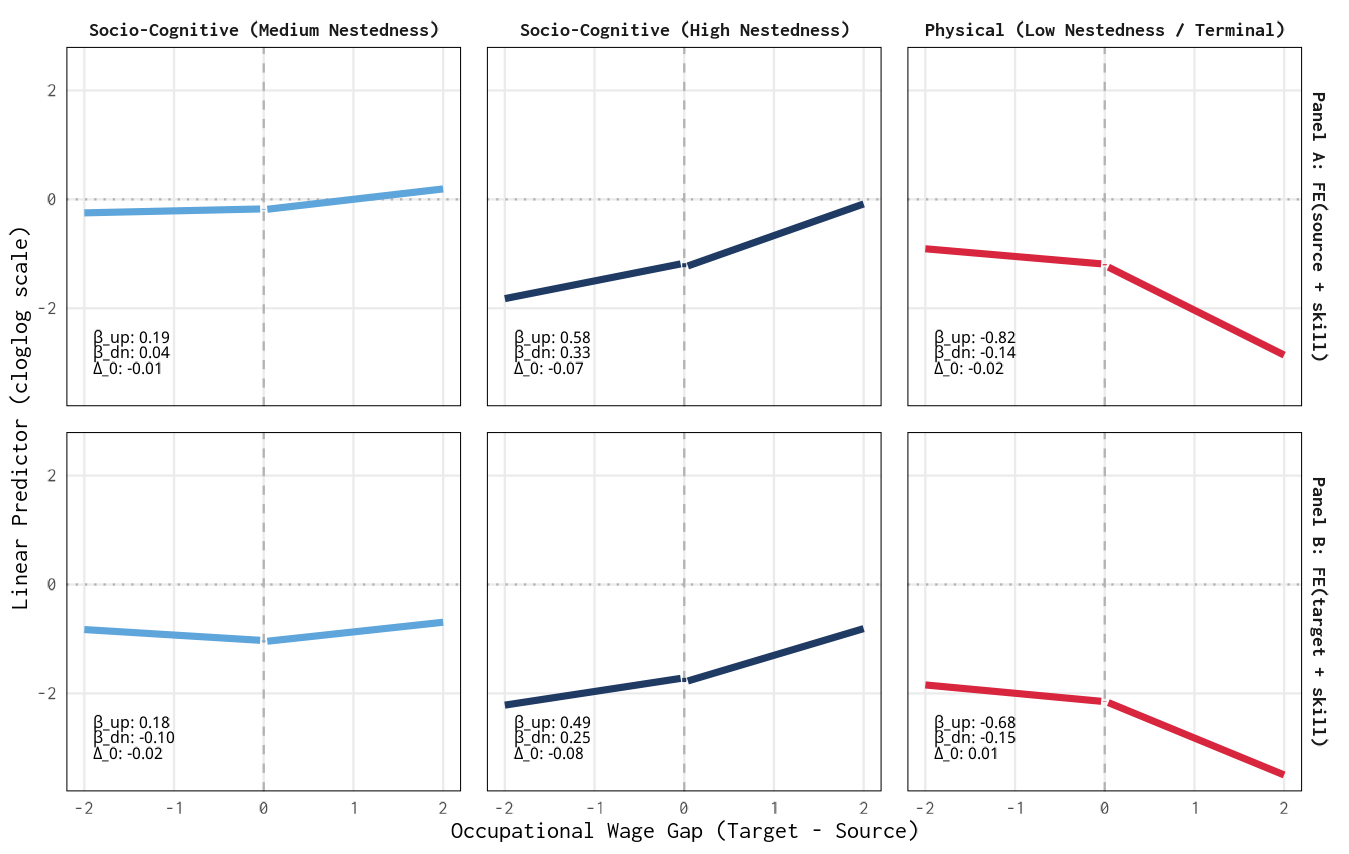
by domain & Nestedness
Why This Happens: Potential Reasons
This asymmetry reflects structural filtering, not chance:
Adoption capacity
High-status occupations have more resources, slack, and organizational capacity to experiment with complex, high-nestedness skills.Market shift
Elite occupations increasingly demand socio-cognitive skills to manage coordination, abstraction, and organizational complexity.Status filtering
High-status occupations actively avoid physical requirements to preserve professional distinction and symbolic boundaries.
Conclusion
Main finding:
Skill diffusion is asymmetric: it pulls socio-cognitive skills upward and pushes physical skills downward.
Key takeaways:
Directional filtering
Physical skills face a barrier that prevents them from entering high-wage occupations.Nestedness matters
Skills that anchor and enable other skills exhibit the strongest asymmetries.Systemic Reproduction
This selective channeling acts as the dynamic engine that maintains and reinforces the labor market’s polarized skill architecture.
Thank You
Roberto Cantillan
Department of Sociology, PUC Chile
rcantillan@uc.cl
Paper and Replication: github.com/rcantillan/skill_diffusion
Backup Slides
B1: Formal Definitions
Revealed Comparative Advantage:
\[\mathrm{RCA}(j,s) = \frac{\mathrm{onet}(j,s)/\sum_{s'}\mathrm{onet}(j,s')}{\sum_{j'}\mathrm{onet}(j',s)/\sum_{j',s''}\mathrm{onet}(j',s'')}\]
Event definitions for skill s:
- Specialists at baseline: RCA greater than 1 at t0
- Users at follow-up: RCA greater than 1 at t1
- New adopters: Users minus Specialists
Directional gaps:
\[\Delta^{\uparrow}_{ij} = \max(0, \text{status}_j - \text{status}_i)\]
\[\Delta^{\downarrow}_{ij} = \max(0, \text{status}_i - \text{status}_j)\]
B2: Nestedness Definition
Contribution to nestedness (cs):
\[c_s = \frac{\mathrm{NODF}_{\text{obs}} - \mathbb{E}[\mathrm{NODF}^{(s)}_{\text{rand}}]}{\mathrm{sd}[\mathrm{NODF}^{(s)}_{\text{rand}}]}\]
Interpretation:
- cs high: Skill acts as scaffolding (analytics, management, communication)
- cs low: Terminal or narrow capability (specific technique)
Reach:
- Size of forward-reachable set in dependency network
- High reach means skill enables many downstream capabilities
In our models:
- Terciles: Low, Mid, High nestedness
- Interact with directional gaps
- High nestedness amplifies ATC asymmetry
B3: Full Coefficient Table
| Term | Coefficient | SE |
|---|---|---|
| Upward (base) | +0.08 | 0.04 |
| Downward (base) | +0.13 | 0.11 |
| Domain: Physical | +0.72 | 0.30 |
| Upward × Physical | −0.42 | 0.07 |
| Downward × Physical | +0.52 | 0.18 |
| Structural distance | −1.90 | 0.20 |
| Distance × Physical | −1.33 | 0.52 |
| Nestedness: Mid | +0.00 | 0.04 |
| Nestedness: High | −0.13 | 0.05 |
| Upward × Nest-Mid | +0.12 | 0. 03 |
| Upward × Nest-High | +0. 07 | 0.04 |
ClogLog link. Two-way FE (source, target). Clustered SE.
B4: Complete Gravity Model Derivation
Step 1: Classic Gravity \[T_{ij} = k \cdot \frac{M_i M_j}{D_{ij}^{\gamma}} \quad \Rightarrow \quad \log \mathbb{E}[T_{ij}] = \beta_0 + \alpha_i + \beta_j - \gamma \log D_{ij}\]
Step 2: Triadic Extension (adding skill \(k\)) \[\lambda_{ijk} \propto \frac{M_i \cdot M_j \cdot S_k}{D_{ij}^{\gamma}} \quad \Rightarrow \quad \log \lambda_{ijk} = \beta_0 + \alpha_i + \beta_j + \delta_k - \gamma \log D_{ij}\]
Step 3: Asymmetric Frictions \[\Delta^{\uparrow}_{ij} = \max(G_{ij}, 0), \quad \Delta^{\downarrow}_{ij} = \max(-G_{ij}, 0)\]
Step 4: Skill Mass via Attributes \[\text{SkillMass}_k = \eta_0 + \eta_D D_k + \eta_N N_k + \eta_{DN} D_k N_k\]
Step 5: Full Specification \[\text{cloglog}\big(\Pr(T_{ijk}=1)\big) = \beta_0 + \alpha_i + \beta_j + \eta_0 + \eta_D D_k + \eta_N N_k + \eta_{DN} D_k N_k + \beta^{\uparrow} \Delta^{\uparrow}_{ij} + \beta^{\downarrow} \Delta^{\downarrow}_{ij}\]
B5: Key Magnitudes
Coefficients (wage gap, cloglog scale):
| Term | Cognitive | Physical | Interaction |
|---|---|---|---|
| Upward | +0.08. | −0.34 | −0.42*** |
| Downward | +0.13 (ns) | +0.65 | +0.52** |
| Distance | −1.90*** | −3.23 | −1.33* |
Interpretation:
- Upward gap slightly boosts cognitive adoption, penalizes physical
- Downward gap has no effect on cognitive, strongly boosts physical
- Distance decay is 70% steeper for physical skills
B6: Robustness Summary
| Test | Specification | Result |
|---|---|---|
| Thresholds | RCA 0.9, 1.0, 1.1 | Pattern unchanged |
| Distances | Shortest path, resistance, cosine | Same relative slopes |
| Periods | 2015-18, 2019-21, 2022-24 | ATC persists |
| Bootstrap | Node-level B=1000 vs clustered SE | Ratio around 1.0 |
| Representation | Skill-skill vs occ-occ network | Ordinal match |
The asymmetry is not an artifact of thresholds, distance measures, or time periods.