Segregación Residencial

Introducción: El Fenómeno de la Segregación Urbana

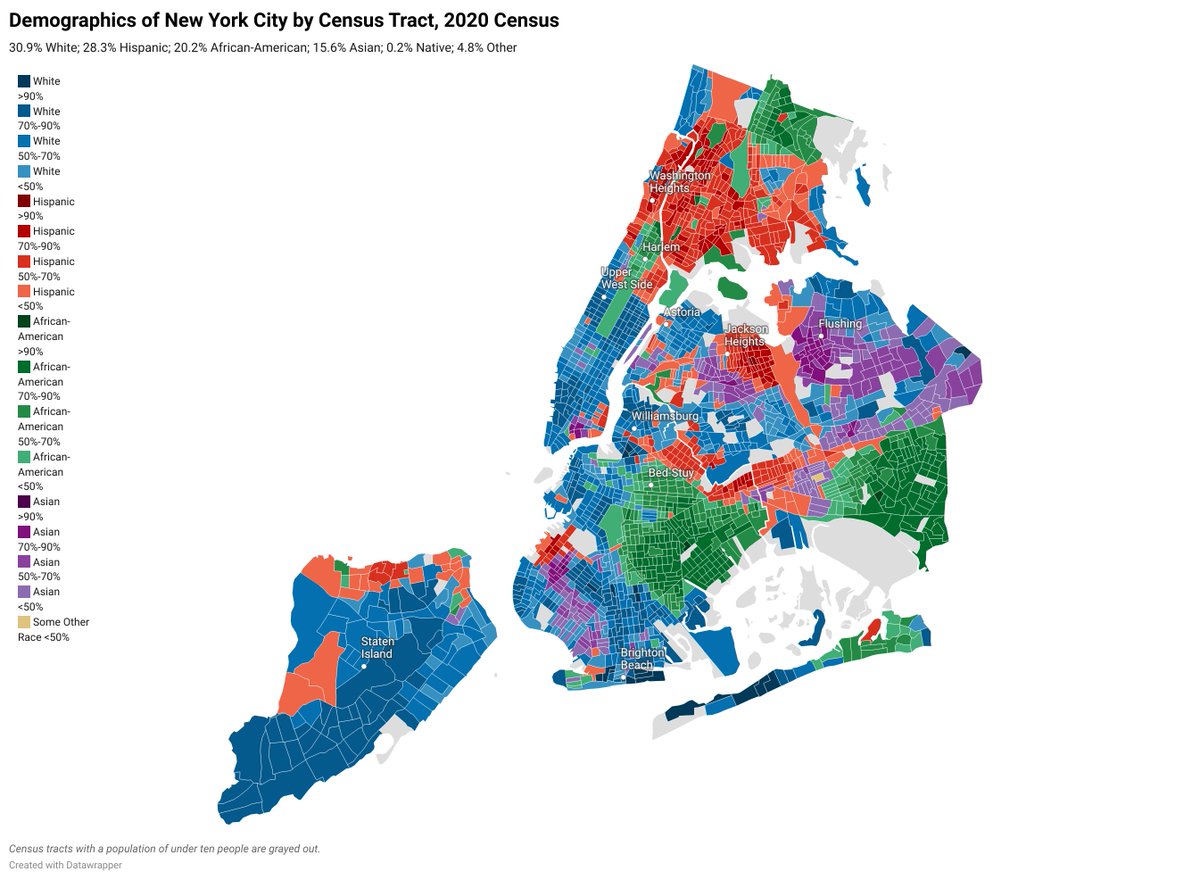
Las ciudades, los barrios y los países suelen estar segregados. Esto significa que las personas de diferentes razas o etnias tienden a estar agrupadas geoespacialmente. Este fenómeno, observable en prácticamente todas las sociedades multiculturales, plantea importantes preguntas sobre sus causas y mecanismos subyacentes.

Por ejemplo, el siguiente mapa muestra los patrones de segregación para la ciudad de NY en el año 2020, donde se pueden observar claramente patrones de agrupamiento espacial por características étnicas:

Marco Teórico: El Modelo de Schelling

Mecanismos de Segregación

Thomas Schelling (1971) identificó tres mecanismos fundamentales que pueden generar segregación:

1. Acción Organizada: Prácticas institucionales discriminatorias, tanto legales como informales
2. Filtros Socioeconómicos: Correlaciones entre etnia y recursos que generan barreras estructurales
3. Preferencias Individuales: Decisiones basadas en la composición del vecindario

Enfoque del Modelo

Aunque Schelling consideraba que los dos primeros mecanismos probablemente eran más importantes, decidió estudiar el tercero para entender cómo incluso preferencias individuales moderadas podrían generar segregación significativa.

Descomposición del Sistema

Antes de construir el modelo, necesitamos descomponer el sistema complejo de segregación urbana en componentes más simples y manejables. Los elementos fundamentales son:

Componentes Espaciales

• Un espacio donde los agentes pueden vivir y moverse
• Ubicaciones discretas que pueden estar ocupadas o vacías
• Vecindarios definidos por proximidad espacial

Componentes de Agentes

• Individuos con una identidad o tipo observable
• Capacidad de percibir su entorno local
• Habilidad para tomar decisiones y moverse
• Preferencias sobre la composición de su vecindario

Componentes Dinámicos

• Reglas de movimiento
• Criterios de satisfacción
• Mecanismos de evaluación del entorno
• Condiciones de equilibrio

Estructura Básica del Modelo

El Espacio

El modelo utiliza una cuadrícula cuadrada por varias razones:

• Es intuitiva de visualizar
• Permite definir vecindarios de manera natural
• Es fácil de implementar computacionalmente
• Proporciona simetría en las relaciones espaciales

Los bordes de la cuadrícula son toroidales, lo que significa que se conectan como si la cuadrícula estuviera envuelta alrededor de un donut. Esto elimina los efectos de borde que podrían distorsionar los resultados.

Los Agentes

Cada agente en el modelo representa a un individuo o familia y tiene:

• Una ubicación en la cuadrícula
• Un tipo o grupo (representado por un color)
• Un umbral de similitud que determina su satisfacción
• La capacidad de evaluar su vecindario y moverse si está insatisfecho

Los Vecindarios

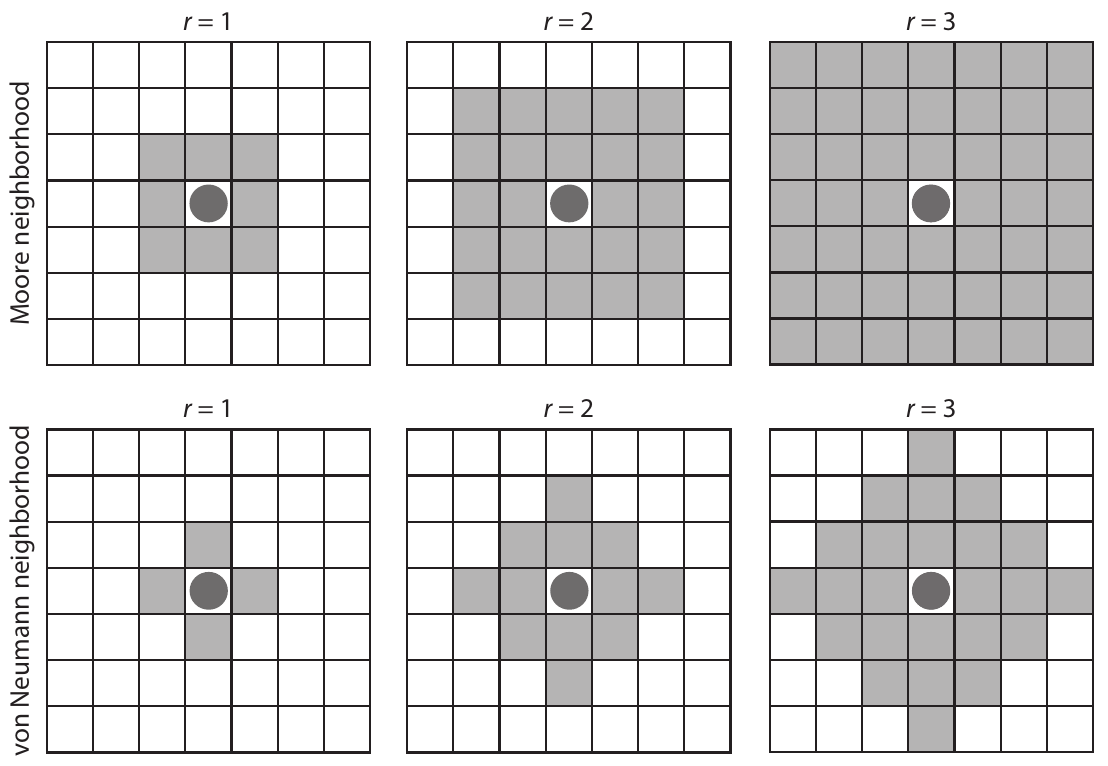
Se define usando el vecindario de Moore:

• Incluye las 8 celdas adyacentes alrededor del agente
• Permite una evaluación local realista
• Es simétrico en todas las direcciones

Inicialización del Modelo

Parámetros Clave

• \(L\): Tamaño de la cuadrícula \((L × L)\)
• \(p\): Densidad de población (proporción de celdas ocupadas)
• \(S\): Umbral de similitud (proporción mínima aceptable de vecinos similares)

Proceso de Inicialización

• Crear una cuadrícula \(L × L\) vacía
• Colocar \(N = p×L²\) agentes aleatoriamente
• Asignar tipos a los agentes con igual probabilidad
• Evaluar la satisfacción inicial de cada agente

Dinámica del Modelo

Reglas de Comportamiento

Cada agente sigue estas reglas en cada paso de tiempo:

Evaluación:

• Cuenta el número total de vecinos
• Calcula la proporción de vecinos similares
• Determina si está satisfecho (proporción ≥ umbral)

Movimiento:

• Si está insatisfecho, busca una nueva ubicación vacía
• Se mueve a una ubicación aleatoria disponible
• Actualiza su estado de satisfacción

Ciclo del Modelo

• Todos los agentes evalúan su satisfacción
• Los agentes insatisfechos se mueven en orden aleatorio
• Se repite hasta alcanzar equilibrio o límite de tiempo

Medidas de Resultado

Similitud Promedio

• Calcula la proporción media de vecinos similares para todos los agentes
• Proporciona una medida cuantitativa de segregación
• Permite comparar diferentes configuraciones del modelo

Infelicidad

• Mide la proporción de agentes insatisfechos
• Indica la estabilidad del sistema
• Ayuda a identificar cuándo se alcanza el equilibrio

Aspectos de Implementación

Estructuras de Datos Necesarias

• Matriz para representar la cuadrícula
• Lista de agentes con sus propiedades
• Variables para seguimiento de medidas globales

Procedimientos Principales

Inicialización:

setup:
  `limpiar_todo`
  `crear_agentes`
  `actualizar_agentes`
  `actualizar_globales`

Dinámica:

paso:
  - si `todos_felices` entonces parar
  - `mover_agentes_infelices`
  - `actualizar_agentes`
  - `actualizar_globales`

Tabla resumen

Componente	Descripción	Detalles de Implementación
Espacio	Cuadrícula cuadrada \(L×L\) con bordes toroidales	Matriz bidimensional; cada celda puede estar vacía u ocupada; conexión toroidal entre bordes opuestos
Agentes	Individuos pertenecientes a dos grupos distintos	Ubicación en la cuadrícula; tipo/color como identificador; estado de satisfacción; capacidad de movimiento
Parámetros Principales	Variables que definen el comportamiento del modelo	\(L\) (tamaño de cuadrícula); \(p\) (densidad de población, \(0 < p < 1\)); \(S\) (umbral de similitud); \(N=pL^2\) (tamaño de población esperado)
Vecindario	Área local que cada agente evalúa	Vecindario de Moore (8 celdas adyacentes); evaluación de proporción de similares; consideración de bordes toroidales
Dinámica	Reglas de evolución del sistema	Evaluación de satisfacción; movimiento de agentes insatisfechos; actualización de estados; repetición hasta equilibrio
Inicialización	Configuración inicial del sistema	Creación de cuadrícula vacía; distribución aleatoria de agentes; asignación aleatoria de tipos; evaluación inicial de satisfacción
Medidas de Resultado	Métricas para evaluar el estado del sistema	Similitud promedio global \((S)\) : \(S̄ = (1/N)∑(si/ni)\), donde: \(si\) = número de vecinos similares del agente \(i\); \(ni\) = número total de vecinos del agente \(i\); \(N\) = número total de agentes; - Proporción de agentes insatisfechos \((U)\), \(U = Nu/N\), donde: \(Nu\) = número de agentes insatisfechos, \(N\) = población total; - Índice de segregación espacial (\(ISE\)), \(ISE = (P - E)/(1 - E)\), donde: \(P\) = proporción observada de vecinos similares, \(E\) = proporción esperada bajo distribución aleatoria; - Tiempo hasta equilibrio (\(Te\)): \(Te\) = número de pasos hasta que \(U\) = 0, Si \(U > 0\) después de 1000 pasos: \(Te = ∞\)
Análisis	Métodos para estudiar el comportamiento del sistema	Múltiples ejecuciones por configuración; barrido sistemático de parámetros; análisis estadístico; identificación de patrones emergentes
Hallazgos Clave	Resultados principales del modelo	Preferencias débiles generan segregación fuerte; densidad afecta significativamente los patrones; sistema alcanza equilibrio rápidamente; patrones emergentes son robustos

Configuración Inicial

Carga de Librerías

Comenzamos cargando las librerías necesarias para nuestro análisis:

# Manipulación de datos y visualización
library(tidyverse)   # Para manejo de datos y gráficos base
library(gganimate)   # Para crear animaciones
library(gifski)      # Para generar GIFs
library(ragg)        # Para mejor renderizado
library(gridExtra)   # Para combinar gráficos
library(viridis)     # Para paletas de colores
library(ggplotify)

# Configuración global de gráficos
theme_set(theme_minimal())

Funciones Base del Modelo

Funciones Auxiliares

Primero definimos funciones auxiliares que serán la base de nuestro modelo:

# FUNCIÓN 1: VERIFICACIÓN DE POSICIÓN VÁLIDA
# Esta función comprueba si una posición (row, col) está dentro de los límites de la cuadrícula
is_valid_position <- function(row, col, n_rows, n_cols) {
  # Parámetros:
  #   row: número de fila a verificar
  #   col: número de columna a verificar
  #   n_rows: número total de filas en la cuadrícula
  #   n_cols: número total de columnas en la cuadrícula
  
  # La función realiza cuatro verificaciones simultáneas:
  # 1. row >= 1     : la fila debe ser al menos 1 (no puede ser 0 o negativa)
  # 2. row <= n_rows: la fila no puede exceder el número total de filas
  # 3. col >= 1     : la columna debe ser al menos 1 (no puede ser 0 o negativa)
  # 4. col <= n_cols: la columna no puede exceder el número total de columnas
  return(row >= 1 && row <= n_rows && col >= 1 && col <= n_cols)
}

# FUNCIÓN 2: OBTENCIÓN DE VECINOS
# Esta función identifica y retorna los valores de todas las celdas vecinas a una posición dada
get_neighbors <- function(grid, row, col) {
  # Parámetros:
  #   grid: matriz que representa la cuadrícula del modelo
  #   row: fila de la celda central
  #   col: columna de la celda central
  
  # Obtener dimensiones de la cuadrícula
  n_rows <- nrow(grid)  # número total de filas
  n_cols <- ncol(grid)  # número total de columnas
  
  # Crear matriz de direcciones para los 8 vecinos posibles
  # expand.grid genera todas las combinaciones posibles de los valores dados
  directions <- expand.grid(
    row = c(-1, 0, 1),  # movimientos posibles en filas (-1:arriba, 0:mismo, 1:abajo)
    col = c(-1, 0, 1)   # movimientos posibles en columnas (-1:izq, 0:mismo, 1:der)
  )
  # Eliminar la posición central (0,0) que representa la celda actual
  directions <- directions[!(directions$row == 0 & directions$col == 0),]
  
  # Obtener valores de los vecinos usando lapply
  # lapply aplica una función a cada fila de directions
  neighbors <- lapply(1:nrow(directions), function(i) {
    # Calcular posición del vecino
    new_row <- row + directions$row[i]  # nueva fila = fila actual + desplazamiento
    new_col <- col + directions$col[i]  # nueva columna = columna actual + desplazamiento
    
    # Verificar si la posición del vecino es válida
    if(is_valid_position(new_row, new_col, n_rows, n_cols)) {
      return(grid[new_row, new_col])  # si es válida, retornar el valor
    } else {
      return(NA)  # si no es válida, retornar NA
    }
  })
  
  # Retornar solo los valores válidos (no NA) como vector
  # unlist convierte la lista en vector
  # !is.na(neighbors) filtra los valores NA
  return(unlist(neighbors[!is.na(neighbors)]))
}

Explicación del Código

La función get_neighbors implementa el concepto de “vecindario de Moore”, considerando los 8 vecinos adyacentes a una celda. Esto es crucial para el modelo ya que representa el entorno social inmediato que influye en las decisiones de los agentes.

Creación del Espacio Social

La siguiente función crea la grilla inicial que representa nuestro espacio social:

# FUNCIÓN: CREACIÓN DE LA CUADRÍCULA DE SCHELLING
# Esta función genera la cuadrícula inicial del modelo de segregación de Schelling

create_schelling_grid <- function(n_rows = 20, n_cols = 20, 
                                p_empty = 0.15, p_ratio = 0.5,
                                exact_counts = FALSE) {
    # PARÁMETROS:
    # n_rows: número de filas (default = 20)
    # n_cols: número de columnas (default = 20)
    # p_empty: proporción deseada de espacios vacíos (default = 0.15 o 15%)
    # p_ratio: proporción deseada del grupo 1 respecto al total de espacios ocupados (default = 0.5 o 50%)
    # exact_counts: boolean que determina si usar conteos exactos o probabilísticos (default = FALSE)
    
    # Calcular el número total de celdas en la cuadrícula
    total_spaces <- n_rows * n_cols
    
    # MÉTODO 1: CONTEOS EXACTOS
    if(exact_counts) {
        # Este método garantiza exactamente las proporciones especificadas
        
        # Calcular el número exacto de celdas para cada tipo
        n_empty <- floor(total_spaces * p_empty)     # Número de celdas vacías
        n_occupied <- total_spaces - n_empty         # Número de celdas ocupadas
        n_group1 <- floor(n_occupied * p_ratio)      # Número de agentes del grupo 1
        n_group2 <- n_occupied - n_group1            # Número de agentes del grupo 2
        
        # Crear vector con valores exactos
        grid_vector <- c(
            rep(1, n_group1),    # Crear n_group1 elementos del grupo 1 (valor = 1)
            rep(2, n_group2),    # Crear n_group2 elementos del grupo 2 (valor = 2)
            rep(0, n_empty)      # Crear n_empty espacios vacíos (valor = 0)
        )
        # Aleatorizar el orden de los elementos
        grid_vector <- sample(grid_vector)
        
    # MÉTODO 2: ASIGNACIÓN PROBABILÍSTICA
    } else {
        # Este método asigna valores basados en probabilidades
        
        # Calcular probabilidades para cada tipo de celda
        prob_empty <- p_empty                    # Probabilidad de celda vacía
        prob_group1 <- (1-p_empty)*p_ratio      # Probabilidad de grupo 1
        prob_group2 <- (1-p_empty)*(1-p_ratio)  # Probabilidad de grupo 2
        
        # Generar vector aleatorio según las probabilidades especificadas
        grid_vector <- sample(
            c(0,1,2),           # Posibles valores: 0=vacío, 1=grupo1, 2=grupo2
            size = total_spaces, # Número total de celdas a generar
            prob = c(prob_empty, prob_group1, prob_group2), # Probabilidades
            replace = TRUE       # Permitir repetición de valores
        )
    }
    
    # Convertir el vector en matriz y retornar
    matrix(grid_vector, nrow = n_rows, ncol = n_cols)
}

Consideraciones Metodológicas Importantes

Esta función implementa dos enfoques diferentes para poblar el espacio:

• Conteos Exactos: Garantiza proporciones específicas de cada grupo, reflejando situaciones donde las proporciones poblacionales son fijas.
• Asignación Probabilística: Introduce variabilidad natural en las proporciones, similar a cómo las poblaciones reales pueden fluctuar.

La elección entre estos métodos puede afectar significativamente la dinámica del modelo.

Cálculo de Satisfacción Individual

El corazón del modelo de Schelling es el mecanismo por el cual los individuos evalúan su satisfacción con su vecindario:

# FUNCIÓN: CÁLCULO DE SATISFACCIÓN
# Esta función determina si un agente está satisfecho con su ubicación actual
# basándose en la composición de su vecindario

calculate_satisfaction <- function(grid, row, col, threshold = 0.375) {
    # PARÁMETROS:
    # grid: matriz que representa la cuadrícula del modelo
    # row: fila del agente a evaluar
    # col: columna del agente a evaluar
    # threshold: umbral mínimo de similitud para estar satisfecho (default = 0.375 o 37.5%)
    
    # CASO ESPECIAL 1: CELDA VACÍA
    # Si la celda está vacía (valor = 0), se considera satisfecha por definición
    # Esto evita procesar celdas vacías y simplifica la lógica del modelo
    if (grid[row, col] == 0) return(TRUE)
    
    # IDENTIFICACIÓN DEL AGENTE Y SU ENTORNO
    # Guardar el tipo del agente actual (1 o 2)
    agent_type <- grid[row, col]
    # Obtener lista de vecinos usando la función get_neighbors
    neighbors <- get_neighbors(grid, row, col)
    
    # ANÁLISIS DEL VECINDARIO
    # Contar vecinos ocupados (excluyendo celdas vacías)
    total_neighbors <- sum(neighbors != 0)
    
    # CASO ESPECIAL 2: SIN VECINOS
    # Si no hay vecinos ocupados, el agente se considera satisfecho
    # Esto evita división por cero y refleja que no hay presión social
    if(total_neighbors == 0) return(TRUE)
    
    # Contar vecinos del mismo tipo que el agente
    same_type_neighbors <- sum(neighbors == agent_type)
    
    # CÁLCULO DE SATISFACCIÓN
    # Calcular la proporción de vecinos similares
    ratio <- same_type_neighbors / total_neighbors
    # Determinar satisfacción comparando con el umbral
    return(ratio >= threshold)
}

Significado Sociológico

Esta función captura una simplificación crucial de la realidad social: la idea de que las personas toman decisiones residenciales basadas en la composición étnica de su vecindario inmediato. El parámetro threshold representa el nivel mínimo de similitud que una persona requiere para estar satisfecha con su ubicación.

El valor predeterminado de 0.375 significa que un agente estará satisfecho incluso siendo minoría en su vecindario, siempre que al menos 37.5% de sus vecinos sean similares a él. Este umbral moderado refleja la hipótesis central de Schelling: incluso preferencias relativamente débiles por similitud pueden generar segregación significativa.

Dinámica de Movilidad

La siguiente función implementa el proceso de reubicación de agentes insatisfechos:

Simulación del Modelo

Función Principal de Simulación

# SIMULACIÓN DEL MODELO DE SEGREGACIÓN DE SCHELLING
# Este conjunto de funciones implementa el modelo clásico de segregación de Schelling,
# que demuestra cómo pequeñas preferencias individuales pueden llevar a 
# patrones emergentes de segregación a nivel macro.

#-------------------------------------------------------------------------------
# FUNCIÓN PRINCIPAL: EJECUTAR SIMULACIÓN COMPLETA
#-------------------------------------------------------------------------------
run_schelling_simulation <- function(n_rows = 20, n_cols = 20, 
                                   p_empty = 0.15, p_ratio = 0.5,
                                   threshold = 0.4, max_steps = 50,
                                   record_metrics = TRUE) {
    # PARÁMETROS DE ENTRADA:
    # n_rows, n_cols: Dimensiones de la cuadrícula (default: 20x20)
    # p_empty: Proporción de espacios vacíos (default: 15%)
    # p_ratio: Proporción entre grupos (default: 50-50)
    # threshold: Umbral de satisfacción (default: 40%)
    # max_steps: Máximo número de iteraciones (default: 50)
    # record_metrics: ¿Registrar métricas? (default: TRUE)
    
    #---------------------------------------------------------------------------
    # FASE 1: INICIALIZACIÓN DEL SISTEMA
    #---------------------------------------------------------------------------
    # Crear la cuadrícula inicial
    grid <- create_schelling_grid(n_rows, n_cols, p_empty, p_ratio)
    # Inicializar lista para almacenar historia de estados
    grid_history <- list(grid)
    
    # Si se solicita registro de métricas, crear estructura de datos
    if(record_metrics) {
        metrics <- data.frame(
            step = 0,                  # Paso de la simulación
            satisfaction_rate = NA,     # Proporción de agentes satisfechos
            segregation_index = NA,     # Índice de segregación
            moves = 0                   # Número de movimientos
        )
        # Calcular métricas iniciales
        metrics[1, 2:3] <- calculate_metrics(grid)
    }
    
    #---------------------------------------------------------------------------
    # FASE 2: BUCLE PRINCIPAL DE SIMULACIÓN
    #---------------------------------------------------------------------------
    for(i in 1:max_steps) {
        # Ejecutar un paso de la simulación
        new_grid <- schelling_step(grid, threshold)
        # Guardar el nuevo estado en el historial
        grid_history[[i + 1]] <- new_grid
        
        # Registrar métricas si está activado
        if(record_metrics) {
            # Obtener métricas del estado actual
            current_metrics <- calculate_metrics(new_grid)
            # Contar número de cambios respecto al estado anterior
            moves <- sum(new_grid != grid)
            # Agregar nueva fila al registro de métricas
            metrics <- rbind(metrics,
                           data.frame(
                               step = i,
                               satisfaction_rate = current_metrics$satisfaction_rate,
                               segregation_index = current_metrics$segregation_index,
                               moves = moves
                           ))
        }
        
        #-----------------------------------------------------------------------
        # FASE 3: VERIFICACIÓN DE EQUILIBRIO
        #-----------------------------------------------------------------------
        # Si no hay cambios entre estados consecutivos, se alcanzó el equilibrio
        if(identical(grid, new_grid)) {
            cat("Equilibrio alcanzado en paso", i, "\n")
            break
        }
        
        # Actualizar estado actual
        grid <- new_grid
    }
    
    #---------------------------------------------------------------------------
    # FASE 4: RETORNO DE RESULTADOS
    #---------------------------------------------------------------------------
    if(record_metrics) {
        return(list(
            grid_history = grid_history,  # Historia completa de estados
            metrics = metrics             # Registro de métricas
        ))
    } else {
        return(grid_history)             # Solo historia de estados
    }
}

#-------------------------------------------------------------------------------
# FUNCIÓN: EJECUTAR UN PASO DE LA SIMULACIÓN (dinámica de movilidad)
#-------------------------------------------------------------------------------
schelling_step <- function(grid, threshold = 0.375) {
    # Obtener dimensiones de la cuadrícula
    n_rows <- nrow(grid)
    n_cols <- ncol(grid)
    # Crear copia para modificar
    new_grid <- grid
    
    #---------------------------------------------------------------------------
    # FASE 1: IDENTIFICACIÓN DE POSICIONES
    #---------------------------------------------------------------------------
    # Encontrar posiciones de todos los agentes (valores != 0)
    agent_positions <- which(grid != 0, arr.ind = TRUE)
    # Encontrar posiciones de espacios vacíos (valores = 0)
    empty_positions <- which(grid == 0, arr.ind = TRUE)
    
    # Verificar si hay espacio para movimientos
    if(nrow(empty_positions) == 0 || nrow(agent_positions) == 0) return(grid)
    
    #---------------------------------------------------------------------------
    # FASE 2: IDENTIFICACIÓN DE AGENTES INSATISFECHOS
    #---------------------------------------------------------------------------
    # Evaluar satisfacción de cada agente
    unsatisfied <- apply(agent_positions, 1, function(pos) {
        !calculate_satisfaction(grid, pos[1], pos[2], threshold)
    })
    
    # Si todos están satisfechos, terminar
    if(!any(unsatisfied)) return(grid)
    
    # Obtener posiciones de agentes insatisfechos
    unsatisfied_positions <- agent_positions[unsatisfied,, drop=FALSE]
    
    #---------------------------------------------------------------------------
    # FASE 3: PROCESO DE REUBICACIÓN
    #---------------------------------------------------------------------------
    if(nrow(unsatisfied_positions) > 0) {
        for(i in 1:nrow(unsatisfied_positions)) {
            # Verificar disponibilidad de espacios
            if(nrow(empty_positions) == 0) break
            
            # Seleccionar nueva ubicación aleatoriamente
            empty_idx <- sample(nrow(empty_positions), 1)
            agent_pos <- unsatisfied_positions[i,]
            empty_pos <- empty_positions[empty_idx,]
            
            # Realizar movimiento
            new_grid[empty_pos[1], empty_pos[2]] <- grid[agent_pos[1], agent_pos[2]]
            new_grid[agent_pos[1], agent_pos[2]] <- 0
            
            # Actualizar lista de espacios disponibles
            empty_positions <- empty_positions[-empty_idx,, drop=FALSE]
        }
    }
    
    return(new_grid)
}

#-------------------------------------------------------------------------------
# FUNCIONES DE MÉTRICAS
#-------------------------------------------------------------------------------
# Función para calcular métricas generales
calculate_metrics <- function(grid) {
    # Inicializar contadores
    satisfied_count <- 0    # Número de agentes satisfechos
    total_agents <- 0      # Número total de agentes
    
    # Recorrer toda la cuadrícula
    for(i in 1:nrow(grid)) {
        for(j in 1:ncol(grid)) {
            if(grid[i,j] != 0) {  # Si hay un agente
                total_agents <- total_agents + 1
                if(calculate_satisfaction(grid, i, j)) {
                    satisfied_count <- satisfied_count + 1
                }
            }
        }
    }
    
    # Calcular métricas finales
    satisfaction_rate <- satisfied_count / total_agents
    segregation_index <- calculate_segregation_index(grid)
    
    return(list(
        satisfaction_rate = satisfaction_rate,
        segregation_index = segregation_index
    ))
}

# Función para calcular índice de segregación
calculate_segregation_index <- function(grid) {
    # Inicializar acumuladores
    segregation_sum <- 0    # Suma de ratios de segregación
    total_pairs <- 0       # Total de pares evaluados
    
    # Recorrer la cuadrícula
    for(i in 1:nrow(grid)) {
        for(j in 1:ncol(grid)) {
            if(grid[i,j] != 0) {  # Si hay un agente
                # Obtener y analizar vecinos
                neighbors <- get_neighbors(grid, i, j)
                similar_neighbors <- sum(neighbors == grid[i,j])
                total_neighbors <- sum(neighbors != 0)
                
                # Calcular ratio si hay vecinos
                if(total_neighbors > 0) {
                    segregation_sum <- segregation_sum + similar_neighbors/total_neighbors
                    total_pairs <- total_pairs + 1
                }
            }
        }
    }
    
    # Retornar índice promedio
    return(segregation_sum / total_pairs)
}

Funciones de visualización

# FUNCIONES DE VISUALIZACIÓN
# Este conjunto de funciones permite visualizar los resultados de la simulación
# de diferentes maneras: gráficos de métricas, estados de la cuadrícula y
# animaciones de la evolución del sistema

#-------------------------------------------------------------------------------
# FUNCIÓN: VISUALIZACIÓN DE MÉTRICAS TEMPORALES
#-------------------------------------------------------------------------------
plot_metrics <- function(metrics) {
    # PROPÓSITO: Crear un gráfico de líneas que muestra la evolución de las
    # métricas (satisfacción y segregación) a lo largo del tiempo
    
    # Transformar datos a formato largo para facilitar la visualización
    metrics_long <- metrics %>%
        pivot_longer(
            cols = c(satisfaction_rate, segregation_index),  # Métricas a visualizar
            names_to = "metric",                            # Nombre de la variable
            values_to = "value"                             # Valor de la métrica
        )
    
    # Crear gráfico usando ggplot2
    ggplot(metrics_long, aes(x = step, y = value, color = metric)) +
        # Añadir líneas para mostrar tendencias
        geom_line(size = 1) +
        # Añadir puntos para mostrar valores específicos
        geom_point(size = 2) +
        # Personalizar colores y etiquetas
        scale_color_manual(
            values = c("#3366CC", "#DC3912"),              # Azul y rojo
            labels = c("Tasa de Satisfacción", "Índice de Segregación"),
            name = "Métrica"
        ) +
        # Usar tema minimalista
        theme_minimal() +
        # Añadir títulos y etiquetas
        labs(
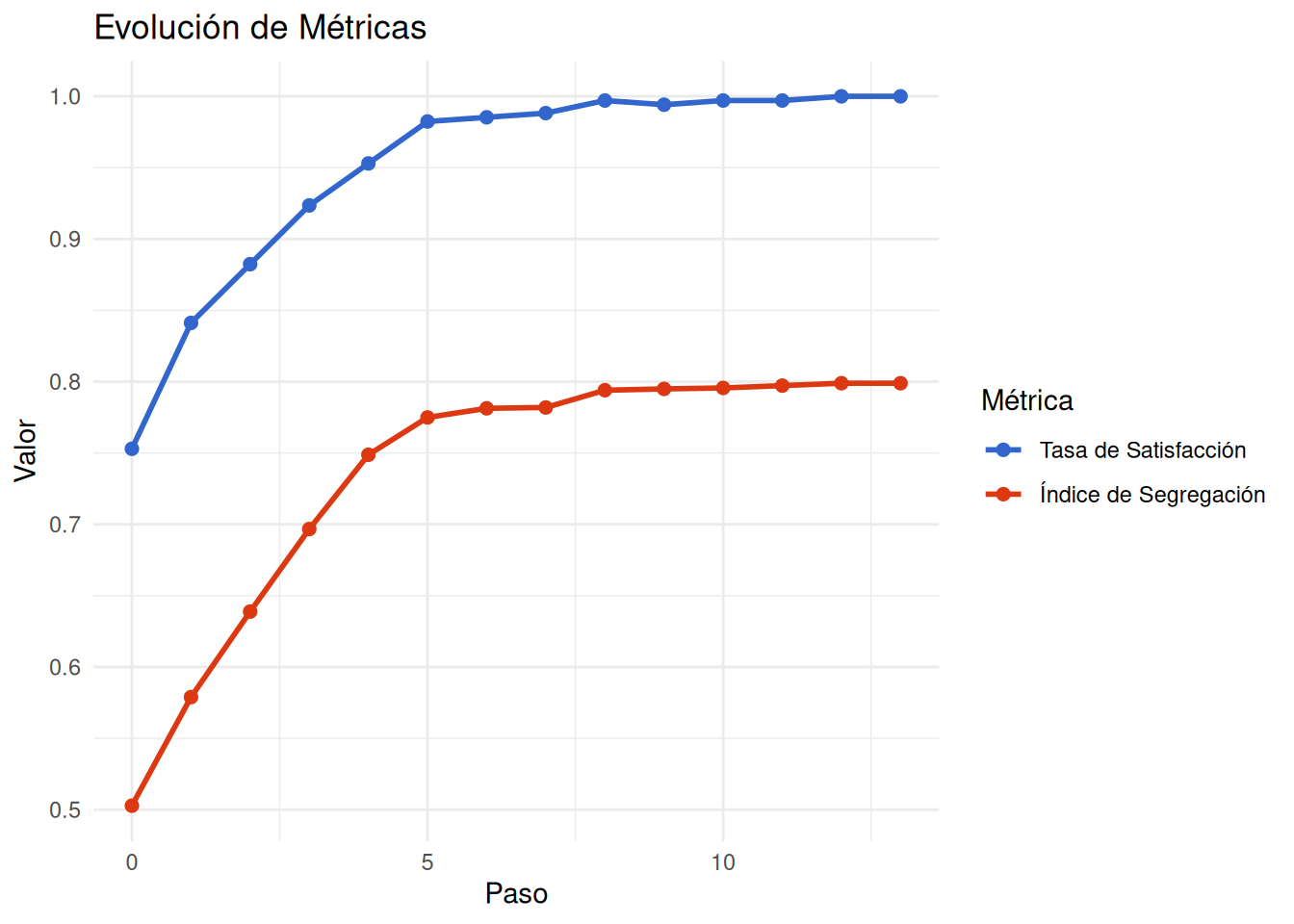
            title = "Evolución de Métricas",
            x = "Paso",
            y = "Valor"
        )
}

#-------------------------------------------------------------------------------
# FUNCIÓN: VISUALIZACIÓN DE ESTADO DE LA CUADRÍCULA
#-------------------------------------------------------------------------------
plot_grid_state <- function(grid, title = NULL) {
    # PROPÓSITO: Crear una visualización de la cuadrícula en un momento específico
    
    # Crear marco de datos con coordenadas y valores
    df <- expand.grid(x = 1:ncol(grid), y = 1:nrow(grid))
    df$value <- as.vector(grid)  # Convertir matriz a vector
    
    # Crear gráfico de la cuadrícula
    ggplot(df, aes(x = x, y = y, fill = factor(value))) +
        # Crear mosaico de celdas
        geom_tile(color = "white", size = 0.5) +
        # Definir colores para cada estado
        scale_fill_manual(
            values = c("white", "#3366CC", "#DC3912"),     # Vacío, Grupo A, Grupo B
            labels = c("Vacío", "Grupo A", "Grupo B"),
            name = "Estado"
        ) +
        # Mantener proporción 1:1
        coord_equal() +
        # Aplicar tema minimalista
        theme_minimal() +
        # Personalizar apariencia
        theme(
            axis.text = element_blank(),      # Ocultar números de ejes
            axis.title = element_blank(),     # Ocultar títulos de ejes
            panel.grid = element_blank()      # Ocultar líneas de cuadrícula
        ) +
        # Añadir título si se proporciona
        ggtitle(title)
}

#-------------------------------------------------------------------------------
# FUNCIÓN: CREACIÓN DE ANIMACIÓN DE LA SIMULACIÓN
#-------------------------------------------------------------------------------
create_simulation_animation <- function(grid_history) {
    # PROPÓSITO: Crear una animación que muestra la evolución del sistema
    
    # Inicializar marco de datos vacío
    df <- data.frame()
    
    # FASE 1: PREPARACIÓN DE DATOS
    # Convertir la historia de estados en un único marco de datos
    for(i in seq_along(grid_history)) {
        # Crear coordenadas para cada celda
        temp_df <- expand.grid(
            x = 1:ncol(grid_history[[1]]),
            y = 1:nrow(grid_history[[1]])
        )
        # Añadir valores y paso temporal
        temp_df$value <- as.vector(grid_history[[i]])
        temp_df$step <- i
        # Combinar con el marco de datos principal
        df <- rbind(df, temp_df)
    }
    
    # FASE 2: CREACIÓN DE LA ANIMACIÓN
    # Crear gráfico base
    p <- ggplot(df, aes(x = x, y = y, fill = factor(value))) +
        # Crear mosaico de celdas
        geom_tile() +
        # Definir colores para cada estado
        scale_fill_manual(
            values = c("white", "#3366CC", "#DC3912"),
            labels = c("Vacío", "Grupo A", "Grupo B"),
            name = "Estado"
        ) +
        # Mantener proporción 1:1
        coord_equal() +
        # Aplicar tema minimalista
        theme_minimal() +
        # Personalizar apariencia
        theme(
            axis.text = element_blank(),
            axis.title = element_blank(),
            panel.grid = element_blank()
        ) +
        # Añadir título dinámico que muestra el paso actual
        labs(title = 'Paso: {frame_time}') +
        # Configurar transición temporal
        transition_time(step)
    
    # FASE 3: RENDERIZAR ANIMACIÓN
    # Crear animación con 2 frames por segundo
    animate(p, nframes = length(grid_history), fps = 2)
}

Ejecución del Modelo y Resultados Iniciales

Simulación Inicial

Comenzamos ejecutando una simulación individual para entender el comportamiento básico del modelo:

# SCRIPT PRINCIPAL DE EJECUCIÓN Y VISUALIZACIÓN
# Este script ejecuta una simulación completa del modelo de Schelling,
# genera visualizaciones y calcula estadísticas resumen

#-------------------------------------------------------------------------------
# FASE 1: PREPARACIÓN Y VERIFICACIÓN
#-------------------------------------------------------------------------------
# Establecer semilla para reproducibilidad de resultados
# Esto garantiza que obtendremos los mismos resultados en cada ejecución
set.seed(123)

# Verificar disponibilidad de funciones necesarias
if(!exists("calculate_metrics") || !exists("calculate_segregation_index")) {
    stop("Las funciones de métricas necesarias no están definidas")
}

#-------------------------------------------------------------------------------
# FASE 2: EJECUCIÓN DE LA SIMULACIÓN
#-------------------------------------------------------------------------------
# Usar tryCatch para manejar posibles errores durante la ejecución
tryCatch({
    # Ejecutar simulación con parámetros específicos
    initial_sim <- run_schelling_simulation(
        n_rows = 20,         # Tamaño de cuadrícula: 20x20
        n_cols = 20,
        p_empty = 0.15,      # 15% de celdas vacías
        p_ratio = 0.5,       # Distribución equitativa entre grupos
        threshold = 0.375,    # Umbral de satisfacción del 37.5%
        max_steps = 50,      # Máximo 50 iteraciones
        record_metrics = TRUE # Registrar métricas durante la simulación
    )
    
    #---------------------------------------------------------------------------
    # FASE 3: VISUALIZACIÓN DE RESULTADOS
    #---------------------------------------------------------------------------
    # Verificar que la simulación fue exitosa
    if(!is.null(initial_sim) && length(initial_sim$grid_history) > 0) {
        
        # PASO 1: Visualizar Estados Inicial y Final
        # Crear gráfico del estado inicial
        initial_state <- plot_grid_state(
            initial_sim$grid_history[[1]], 
            "Estado Inicial del Sistema"
        )
        
        # Crear gráfico del estado final
        final_state <- plot_grid_state(
            initial_sim$grid_history[[length(initial_sim$grid_history)]], 
            "Estado Final del Sistema"
        )
        
        # Mostrar ambos estados lado a lado
        if(require(gridExtra)) {
            grid.arrange(initial_state, final_state, ncol = 2)
        }
        
        # PASO 2: Crear y Guardar Animación
        simulation_animation <- create_simulation_animation(initial_sim$grid_history)
        # Guardar animación en archivo GIF
        anim_save("segregacion_schelling_01.gif", simulation_animation)
        # Mostrar animación en el visor
        print(simulation_animation)
        
        # PASO 3: Análisis de Métricas
        if(nrow(initial_sim$metrics) > 0) {
            # Crear gráfico de evolución de métricas
            metrics_plot <- plot_metrics(initial_sim$metrics)
            print(metrics_plot)
            
            # PASO 4: Análisis Estadístico
            # Calcular estadísticas resumen
            summary_stats <- initial_sim$metrics %>%
                summarise(
                    pasos_equilibrio = n(),           # Número de pasos hasta equilibrio
                    segregacion_final = last(segregation_index),  # Segregación final
                    satisfaccion_final = last(satisfaction_rate), # Satisfacción final
                    movimientos_totales = sum(moves)  # Total de movimientos
                )
            
            # Mostrar resultados
            print("Estadísticas de la simulación inicial:")
            print(summary_stats)
        }
    }
}, error = function(e) {
    # Manejo de errores: mostrar mensaje informativo
    message("Error en la simulación: ", e$message)
})

Equilibrio alcanzado en paso 13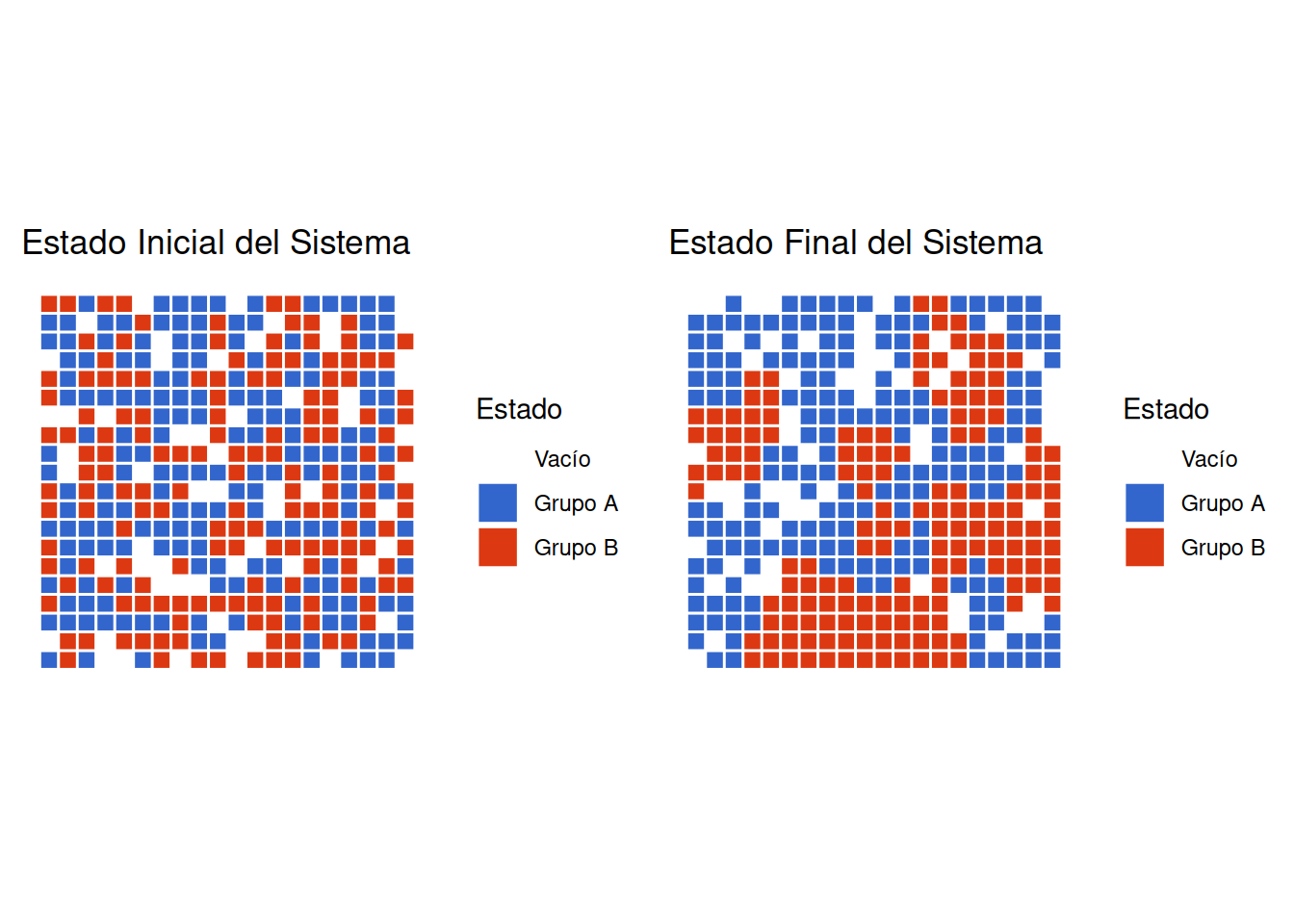 

[1] "Estadísticas de la simulación inicial:"
  pasos_equilibrio segregacion_final satisfaccion_final movimientos_totales
1               14         0.7989076                  1                 432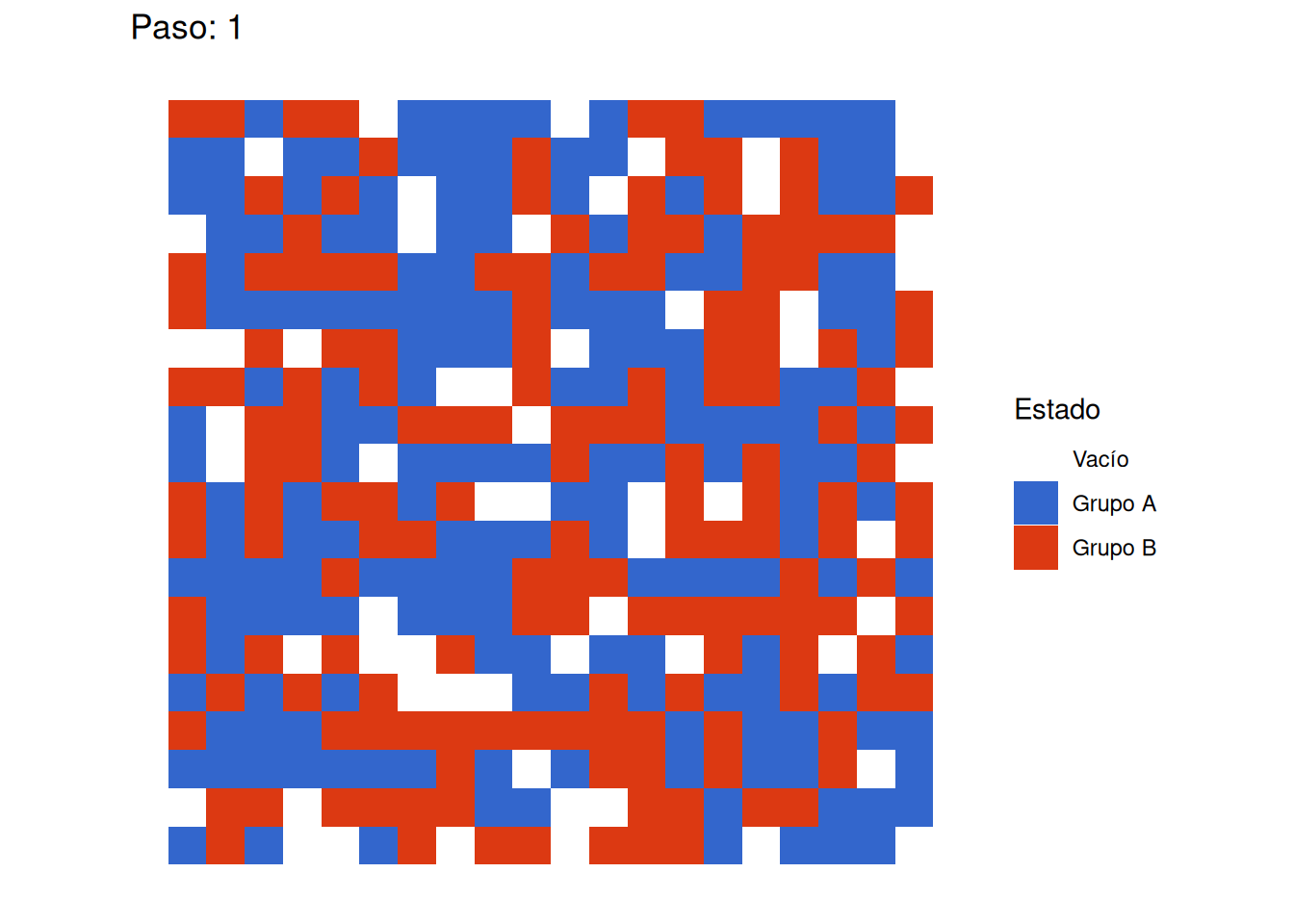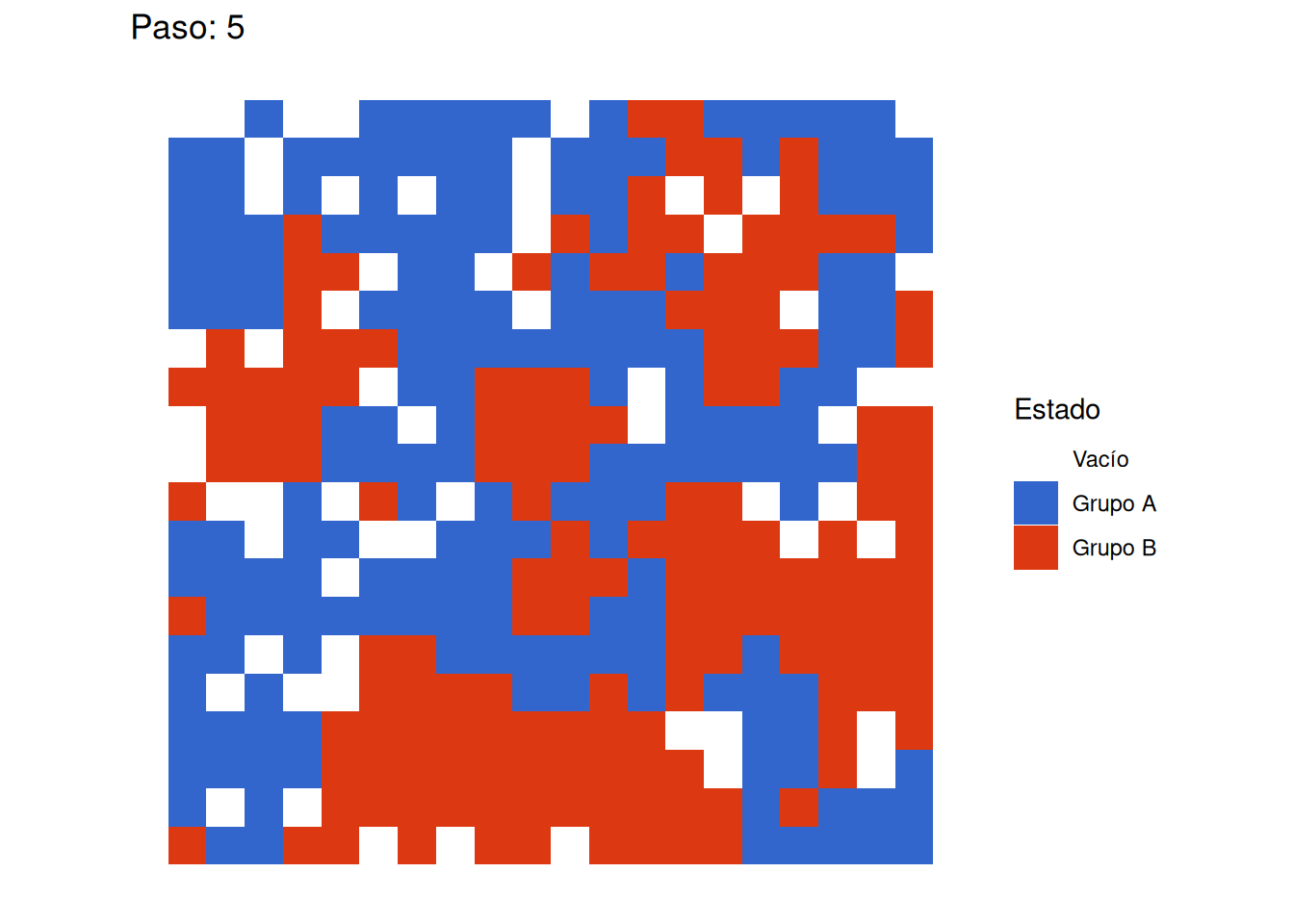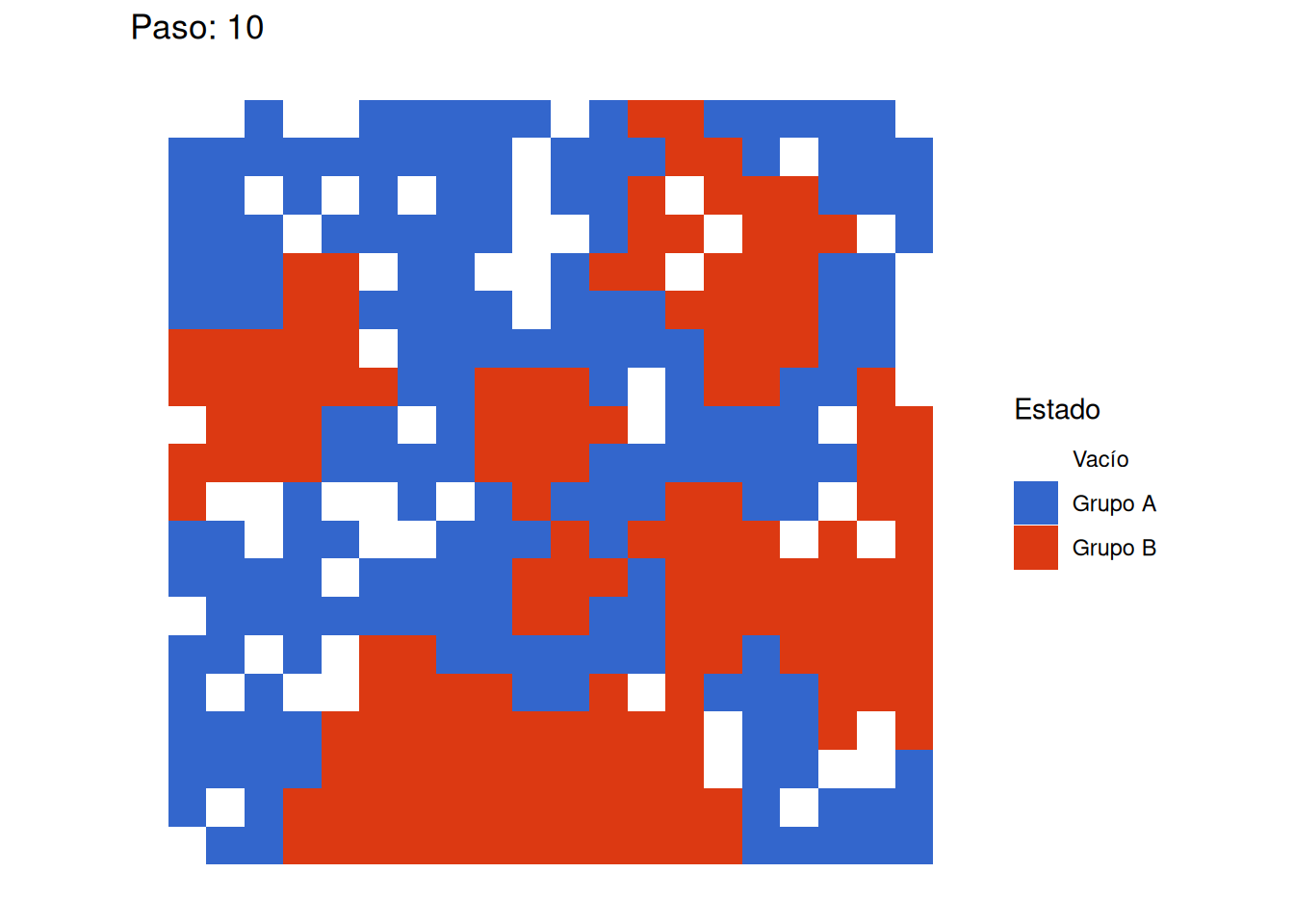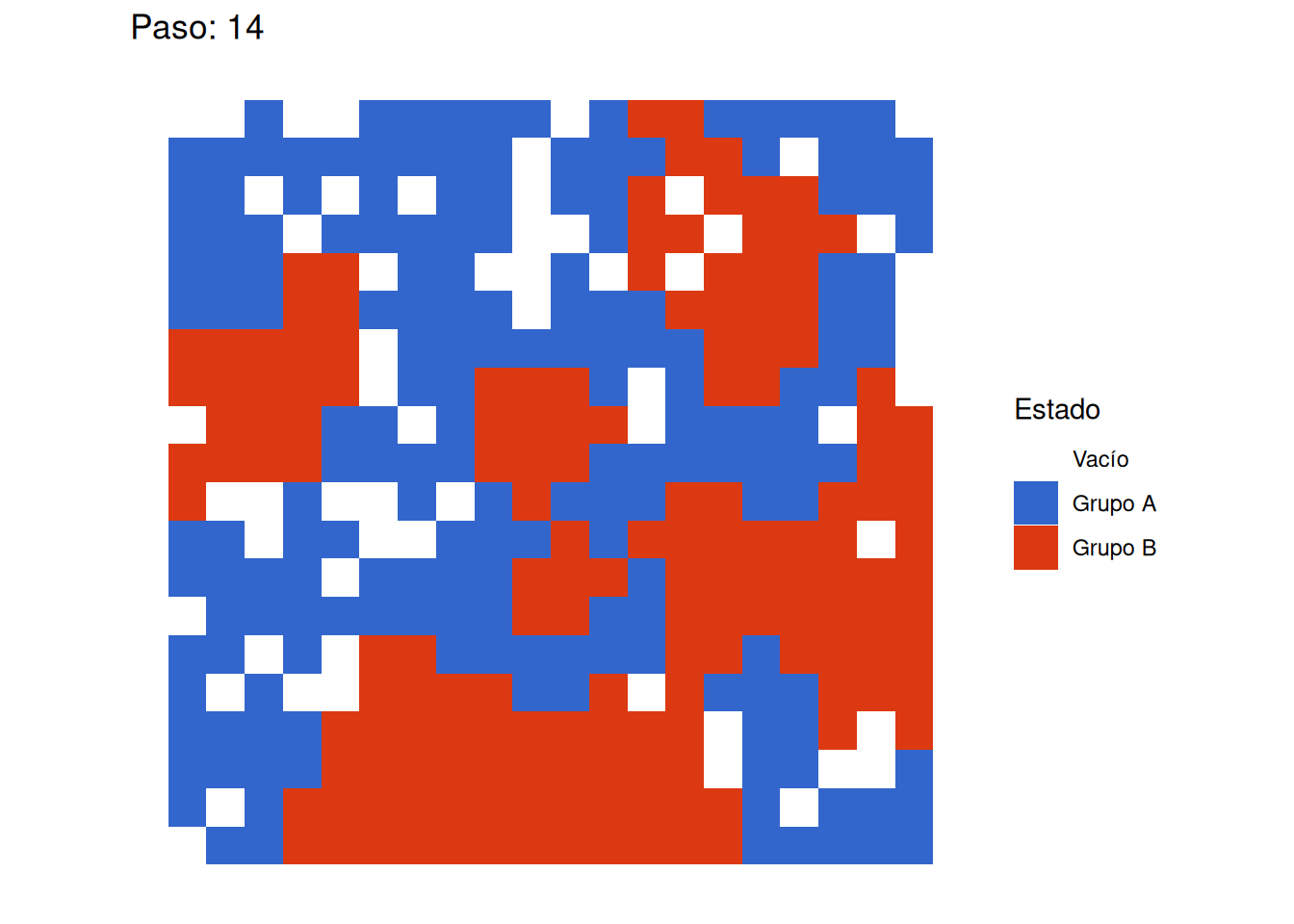

Animación de la Simulación de Schelling

Análisis de Sensibilidad como Experimento

Fundamentos del Experimento

El análisis de sensibilidad que realizaremos constituye un verdadero experimento por varias razones fundamentales:

1. Control de Variables: Manipulamos sistemáticamente variables independientes específicas (threshold y density) mientras mantenemos constantes otros parámetros del modelo.

2. Medición de Resultados: Observamos cómo estas manipulaciones afectan una variable dependiente clara (el índice de segregación).

3. Replicabilidad: Cada combinación de parámetros se repite múltiples veces para asegurar que los resultados no son producto del azar.

4. Escenarios Contrafácticos: Quizás lo más importante, este experimento nos permite explorar “qué pasaría si…” - escenarios que no podríamos observar en el mundo real. Por ejemplo, podemos preguntarnos: ¿Qué pasaría si todas las personas estuvieran dispuestas a ser minoría en sus vecindarios? ¿Qué sucedería si la densidad poblacional fuera mucho menor?

¿Por qué es un Experimento?

A diferencia de la simple observación, este análisis nos permite: - Establecer relaciones causales entre parámetros y resultados - Aislar el efecto de variables específicas - Explorar condiciones que no existen naturalmente - Replicar resultados bajo condiciones controladas

#===============================================================================
# ANÁLISIS DE SENSIBILIDAD DEL MODELO DE SCHELLING
# Este script implementa un análisis sistemático de cómo diferentes parámetros
# afectan el comportamiento del modelo
#===============================================================================

#-------------------------------------------------------------------------------
# FUNCIÓN: ANÁLISIS DE SENSIBILIDAD
#-------------------------------------------------------------------------------
run_sensitivity_analysis <- function(
    thresholds = seq(0.2, 0.8, by = 0.1),  # Rango de umbrales de satisfacción
    densities = seq(0.6, 0.9, by = 0.1),   # Rango de densidades poblacionales
    n_reps = 5,                            # Número de repeticiones
    grid_size = 20) {                      # Tamaño de la cuadrícula
    
    # FASE 1: PREPARACIÓN DEL EXPERIMENTO
    # Crear todas las combinaciones posibles de parámetros
    results <- expand.grid(
        threshold = thresholds,    # Umbrales de satisfacción a probar
        density = densities,       # Densidades poblacionales a probar
        rep = 1:n_reps            # Repeticiones para cada combinación
    )
    
    # Inicializar columnas para métricas de resultado
    results$segregation <- NA           # Índice de segregación final
    results$satisfaction <- NA          # Tasa de satisfacción final
    results$steps_to_equilibrium <- NA  # Pasos hasta equilibrio
    results$total_moves <- NA          # Total de movimientos
    
    # Configurar seguimiento de progreso
    n_total <- nrow(results)
    cat("Iniciando análisis de sensibilidad...\n")
    
    # FASE 2: EJECUCIÓN DE SIMULACIONES
    for(i in 1:nrow(results)) {
        tryCatch({
            # Calcular proporción de celdas vacías
            current_p_empty <- 1 - results$density[i]
            
            # Ejecutar simulación con parámetros actuales
            sim <- run_schelling_simulation(
                n_rows = grid_size,
                n_cols = grid_size,
                p_empty = current_p_empty,
                p_ratio = 0.5,              # Grupos de igual tamaño
                threshold = results$threshold[i],
                max_steps = 100,
                record_metrics = TRUE
            )
            
            # Registrar resultados si la simulación fue exitosa
            if(!is.null(sim$metrics) && nrow(sim$metrics) > 0) {
                final_metrics <- tail(sim$metrics, 1)
                results$segregation[i] <- final_metrics$segregation_index
                results$satisfaction[i] <- final_metrics$satisfaction_rate
                results$steps_to_equilibrium[i] <- nrow(sim$metrics)
                results$total_moves[i] <- sum(sim$metrics$moves)
            }
            
        }, error = function(e) {
            warning(sprintf("Error en iteración %d: %s", i, e$message))
        })
        
        # Actualizar barra de progreso
        if(i %% 10 == 0 || i == n_total) {
            cat(sprintf("\rProgreso: %d%%", round(100 * i/n_total)))
        }
    }
    
    cat("\nAnálisis completado.\n")
    
    # Eliminar filas con datos faltantes
    results <- results[complete.cases(results), ]
    
    return(results)
}

#-------------------------------------------------------------------------------
# FUNCIÓN: VISUALIZACIÓN DE RESULTADOS
#-------------------------------------------------------------------------------
plot_sensitivity <- function(results) {
    # Calcular estadísticas resumen por combinación de parámetros
    summary_stats <- results %>%
        group_by(threshold, density) %>%
        summarise(
            mean_seg = mean(segregation),  # Segregación media
            sd_seg = sd(segregation),      # Desviación estándar
            .groups = 'drop'
        )
    
    # Crear mapa de calor
    ggplot(summary_stats, aes(x = threshold, y = density, fill = mean_seg)) +
        geom_tile() +                # Usar tiles para mapa de calor
        scale_fill_viridis() +       # Escala de colores viridis
        theme_minimal() +            # Tema minimalista
        labs(
            title = "Análisis de Sensibilidad",
            x = "Umbral de Satisfacción",
            y = "Densidad Poblacional",
            fill = "Segregación\nMedia"
        )
}

#-------------------------------------------------------------------------------
# EJECUCIÓN DEL ANÁLISIS
#-------------------------------------------------------------------------------
# Ejecutar análisis de sensibilidad
sensitivity_results <- run_sensitivity_analysis(
    thresholds = seq(0.2, 0.8, by = 0.1),  # Umbrales del 20% al 80%
    densities = seq(0.6, 0.9, by = 0.1),   # Densidades del 60% al 90%
    n_reps = 5,                            # 5 repeticiones por combinación
    grid_size = 20                         # Cuadrícula 20x20
)

Iniciando análisis de sensibilidad...
Equilibrio alcanzado en paso 6 
Equilibrio alcanzado en paso 8 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 8 
Equilibrio alcanzado en paso 15 
Equilibrio alcanzado en paso 29 
Equilibrio alcanzado en paso 4 
Equilibrio alcanzado en paso 10 
Equilibrio alcanzado en paso 14 

Progreso: 7%Equilibrio alcanzado en paso 14 
Equilibrio alcanzado en paso 32 
Equilibrio alcanzado en paso 54 
Equilibrio alcanzado en paso 7 
Equilibrio alcanzado en paso 7 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 27 
Equilibrio alcanzado en paso 66 

Progreso: 14%Equilibrio alcanzado en paso 4 
Equilibrio alcanzado en paso 13 
Equilibrio alcanzado en paso 16 
Equilibrio alcanzado en paso 22 
Equilibrio alcanzado en paso 47 
Equilibrio alcanzado en paso 5 
Equilibrio alcanzado en paso 9 

Progreso: 21%Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 12 
Equilibrio alcanzado en paso 18 
Equilibrio alcanzado en paso 44 
Equilibrio alcanzado en paso 5 
Equilibrio alcanzado en paso 8 
Equilibrio alcanzado en paso 16 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 26 

Progreso: 29%Equilibrio alcanzado en paso 33 
Equilibrio alcanzado en paso 4 
Equilibrio alcanzado en paso 8 
Equilibrio alcanzado en paso 15 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 39 
Equilibrio alcanzado en paso 57 
Equilibrio alcanzado en paso 4 

Progreso: 36%Equilibrio alcanzado en paso 19 
Equilibrio alcanzado en paso 24 
Equilibrio alcanzado en paso 58 
Equilibrio alcanzado en paso 5 
Equilibrio alcanzado en paso 15 
Equilibrio alcanzado en paso 13 
Equilibrio alcanzado en paso 13 

Progreso: 43%Equilibrio alcanzado en paso 23 
Equilibrio alcanzado en paso 38 
Equilibrio alcanzado en paso 6 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 10 
Equilibrio alcanzado en paso 10 
Equilibrio alcanzado en paso 24 
Equilibrio alcanzado en paso 57 

Progreso: 50%Equilibrio alcanzado en paso 4 
Equilibrio alcanzado en paso 8 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 12 
Equilibrio alcanzado en paso 29 
Equilibrio alcanzado en paso 67 
Equilibrio alcanzado en paso 9 
Equilibrio alcanzado en paso 12 
Equilibrio alcanzado en paso 15 

Progreso: 57%Equilibrio alcanzado en paso 22 
Equilibrio alcanzado en paso 54 
Equilibrio alcanzado en paso 5 
Equilibrio alcanzado en paso 9 
Equilibrio alcanzado en paso 10 
Equilibrio alcanzado en paso 8 
Equilibrio alcanzado en paso 20 
Equilibrio alcanzado en paso 31 

Progreso: 64%Equilibrio alcanzado en paso 4 
Equilibrio alcanzado en paso 8 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 12 
Equilibrio alcanzado en paso 21 
Equilibrio alcanzado en paso 41 
Equilibrio alcanzado en paso 4 
Equilibrio alcanzado en paso 9 

Progreso: 71%Equilibrio alcanzado en paso 10 
Equilibrio alcanzado en paso 12 
Equilibrio alcanzado en paso 20 
Equilibrio alcanzado en paso 73 
Equilibrio alcanzado en paso 4 
Equilibrio alcanzado en paso 13 
Equilibrio alcanzado en paso 10 
Equilibrio alcanzado en paso 27 

Progreso: 79%Equilibrio alcanzado en paso 4 
Equilibrio alcanzado en paso 6 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 7 
Equilibrio alcanzado en paso 22 
Equilibrio alcanzado en paso 46 
Equilibrio alcanzado en paso 5 

Progreso: 86%Equilibrio alcanzado en paso 10 
Equilibrio alcanzado en paso 6 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 21 
Equilibrio alcanzado en paso 56 
Equilibrio alcanzado en paso 4 
Equilibrio alcanzado en paso 10 
Equilibrio alcanzado en paso 11 
Equilibrio alcanzado en paso 13 

Progreso: 93%Equilibrio alcanzado en paso 43 
Equilibrio alcanzado en paso 78 
Equilibrio alcanzado en paso 5 
Equilibrio alcanzado en paso 18 
Equilibrio alcanzado en paso 21 
Equilibrio alcanzado en paso 86 

Progreso: 100%
Análisis completado.

# Visualizar resultados
sensitivity_plot <- plot_sensitivity(sensitivity_results)
print(sensitivity_plot)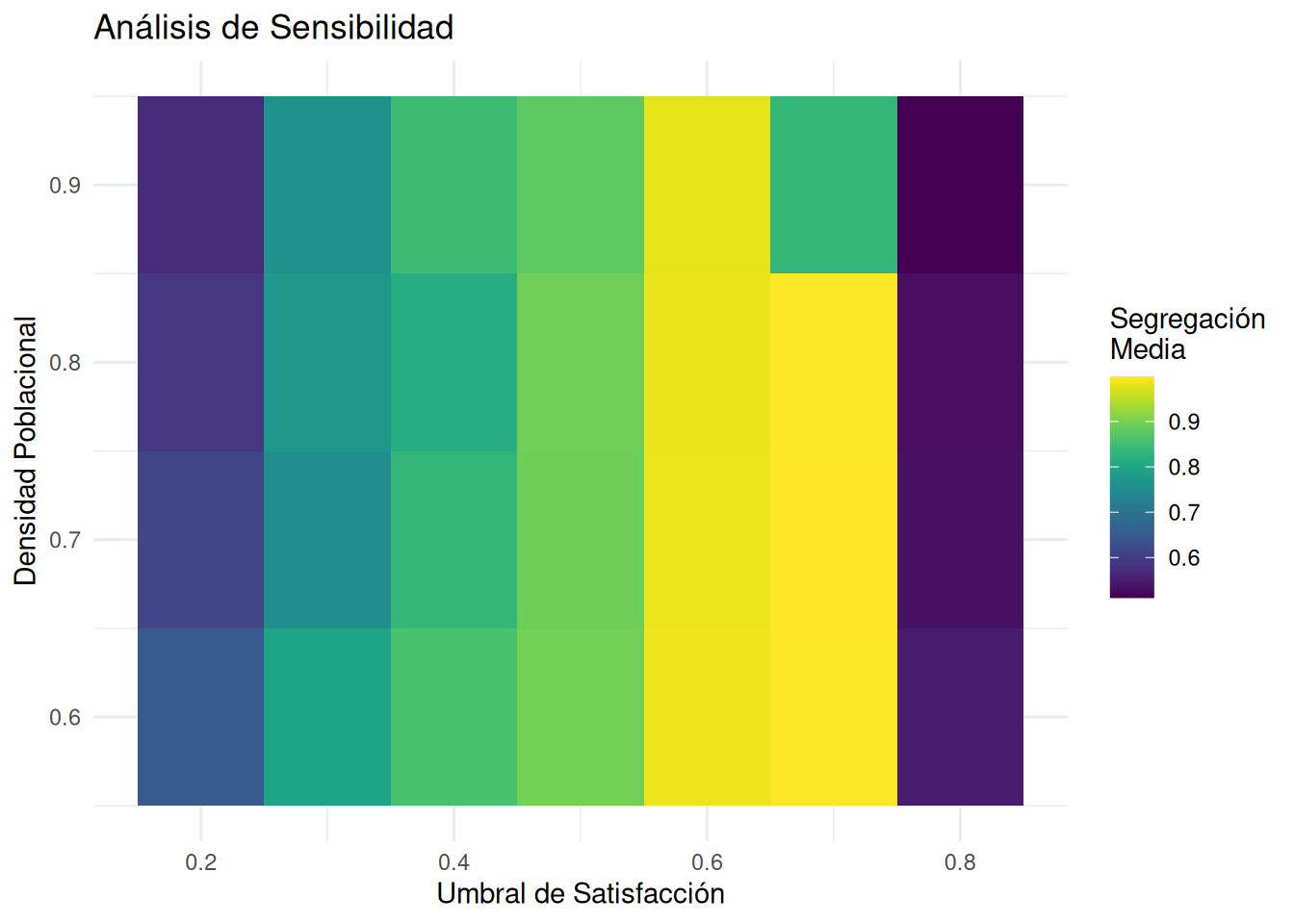

# FASE 3: ANÁLISIS ESTADÍSTICO
# Calcular estadísticas resumen detalladas
summary_stats <- sensitivity_results %>%
    group_by(threshold, density) %>%
    summarise(
        mean_segregation = mean(segregation, na.rm = TRUE),
        sd_segregation = sd(segregation, na.rm = TRUE),
        mean_steps = mean(steps_to_equilibrium, na.rm = TRUE),
        mean_satisfaction = mean(satisfaction, na.rm = TRUE),
        n = n(),
        .groups = 'drop'
    )

print("Resumen estadístico del análisis de sensibilidad:")

[1] "Resumen estadístico del análisis de sensibilidad:"

print(summary_stats)

# A tibble: 28 × 7
   threshold density mean_segregation sd_segregation mean_steps
       <dbl>   <dbl>            <dbl>          <dbl>      <dbl>
 1       0.2     0.6            0.649         0.0200        6  
 2       0.2     0.7            0.613         0.0396        5.8
 3       0.2     0.8            0.589         0.0174        5.6
 4       0.2     0.9            0.569         0.0299        6.2
 5       0.3     0.6            0.796         0.0141       10.4
 6       0.3     0.7            0.749         0.0159       10.4
 7       0.3     0.8            0.771         0.0178        9.4
 8       0.3     0.9            0.755         0.0230       48.6
 9       0.4     0.6            0.859         0.0355       12.2
10       0.4     0.7            0.834         0.0221       12.4
# ℹ 18 more rows
# ℹ 2 more variables: mean_satisfaction <dbl>, n <int>

Interpretación de Resultados Experimentales

El experimento revela varios hallazgos importantes:

• Efecto del Umbral: A medida que aumenta el umbral de satisfacción requerido, la segregación tiende a aumentar, con un punto de inflexión notable alrededor de 0.5-0.6.
• Efecto de la Densidad: Densidades poblacionales más altas tienden a reducir la segregación, posiblemente porque limitan las opciones de reubicación.
• Interacción: El experimento revela una interacción compleja entre densidad y umbral - la influencia del umbral de satisfacción es más pronunciada en densidades medias.

Valor de los Escenarios Contrafácticos

Este experimento nos permite explorar condiciones que serían éticamente imposibles o logísticamente inviables de estudiar en el mundo real. Por ejemplo, podemos examinar qué sucedería si todos los residentes tuvieran exactamente el mismo nivel de tolerancia, algo que nunca ocurre en la realidad pero que nos ayuda a entender el rol de las preferencias individuales en la segregación.

Discusión de Resultados

Análisis de la Simulación Inicial

Los resultados de nuestra simulación inicial revelan varios patrones importantes:

1. Emergencia de Segregación: Incluso con un umbral de satisfacción moderado (0.375), que permite a los agentes ser minoría en sus vecindarios, observamos la formación de clusters claramente definidos. Esto confirma la hipótesis central de Schelling sobre cómo preferencias individuales moderadas pueden generar patrones marcados de segregación a nivel macro.

2. Dinámica Temporal: La evolución de las métricas muestra que:

   • La segregación aumenta rápidamente en las etapas iniciales
   • Existe un punto de inflexión después del cual los cambios son más graduales
   • El sistema eventualmente alcanza un estado de equilibrio

3. Estabilidad del Sistema: El equilibrio alcanzado es estable, lo que significa que una vez que los agentes están satisfechos con sus vecindarios, no hay más movimientos. Esto sugiere que los patrones de segregación, una vez establecidos, pueden ser difíciles de revertir sin intervenciones externas.

Interpretación del Análisis de Sensibilidad

El análisis de sensibilidad revela relaciones complejas entre los parámetros del modelo y sus resultados:

Efecto del Umbral de Satisfacción

• Relación No Lineal: El aumento en el umbral de satisfacción no produce un incremento lineal en la segregación. Existen puntos críticos donde pequeños cambios en las preferencias pueden causar grandes cambios en los patrones de segregación.
• Umbral Crítico: Alrededor de 0.5-0.6, observamos un punto de inflexión particular, donde la segregación aumenta dramáticamente. Esto sugiere la existencia de un “punto de no retorno” en las preferencias individuales.

Impacto de la Densidad Poblacional

• Restricción Estructural: La densidad actúa como una restricción importante que puede amplificar o mitigar el efecto de las preferencias individuales.
• Efecto Moderador: Densidades más altas tienden a reducir la segregación, posiblemente porque limitan las opciones de reubicación disponibles.

Interacción entre Variables

• Efectos Combinados: La influencia del umbral de satisfacción es más pronunciada en densidades medias, sugiriendo una interacción compleja entre estos parámetros.
• Variabilidad en Resultados: La desviación estándar en los resultados varía según la combinación de parámetros, indicando que algunos escenarios son más predecibles que otros.

Limitaciones del Modelo

Es importante reconocer varias limitaciones significativas en nuestro análisis:

1. Simplificación de la Realidad Social
   • El modelo reduce las decisiones residenciales a un único factor
   • No considera factores económicos, sociales o institucionales
   • Asume perfecta movilidad sin costos
2. Homogeneidad de Preferencias
   • Todos los agentes del mismo grupo tienen idénticas preferencias
   • No hay variación temporal en las preferencias
   • No considera la posibilidad de preferencias adaptativas
3. Restricciones del Espacio
   • La grilla es homogénea sin características geográficas
   • No hay variación en la calidad o deseabilidad de las ubicaciones
   • El tamaño del vecindario es fijo
4. Limitaciones Computacionales
   • El análisis de sensibilidad está limitado a un conjunto discreto de valores
   • El tamaño de la grilla y el número de repeticiones están restringidos por recursos computacionales

Conclusiones y Futuras Direcciones

Principales Hallazgos

Nuestro análisis computacional del modelo de Schelling ha producido tres conclusiones principales:

1. Emergencia de Segregación: Confirmamos que preferencias individuales moderadas pueden producir patrones significativos de segregación a nivel macro, sin necesidad de actitudes extremas o políticas discriminatorias.

2. Complejidad del Sistema: La relación entre preferencias individuales y resultados colectivos es no lineal y muestra puntos críticos donde pequeños cambios pueden tener grandes efectos.

3. Papel de las Restricciones: La densidad poblacional actúa como una restricción estructural importante que puede modular el efecto de las preferencias individuales.